Геометричний закон.
Закон подається формулою:
Геометричний закон розподілу має частота настання події у схемі незалежних повторних випробувань, якщо вони проводяться до першого настання події. У формулі р — імовірність настання події в кожному випробуванні. Геометричний закон розподілу застосовується у задачах статистичного контролю якості і теорії надійності. Числові характеристики розподілу:
_________________________________
46. Розподіл Х2. Розглядаємо послідовність Якщо
Числові характеристики розподілу: M(X)=n. D(X)=2n. _________________________________ 47. Математичне сподівання і дисперсія при нормальному розподілу. Нормальний розподіл — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності
Нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Математичне сподівання нормального розподілу дорівнює параметру а: М(Х) = а. Дисперсія при нормальному розподілі: D(Х) = σ2. _________________________________ 48. Ймовірність влучення в заданий інтервал при нормальному розподілі. Нормальний розподіл — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності
Ймовірність влучення в заданий інтервал при нормальному розподілі: Р (α<х<β) = Ф де Ф(х) = _________________________________
49. Математичне сподівання і дисперсія при показовому розподілу. Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)
Випадкові величини з таким законом розподілу широко застосовуються в задачах з теорії надійності та теорії масового обслуговування. Числові характеристики:
_________________________________
50. Ймовірність влучення в заданий інтервал при показовому розподілі. Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)
Функція розподілу показового закону:
Ймовірність влучення в заданий інтервал при показовому розподілі: Р(а < X < b) = F(b) – F(a) =1 – e –λb – (1 – e -λa ) = e -λa – e -λb _________________________________
51. Показовий розподіл. Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)
Показовий розподіл визначається одним параметром λ. Ця особливість має перевагу в порівнянні з розподілами, що залежать від більшого числа параметрів. Функція розподілу показового закону:
_________________________________
52. Елементи математичної статистики. Вибірковий метод. Центральним поняттям статистики є поняття статистичної сукупності, як маси деяких однорідних елементів, що відрізняються між собою за певними ознаками. Одиниці сукупності, з яких складається статистична сукупність, надалі будемо називати елементами цієї сукупності. Встановлення статистичних закономірностей, щодо масових випадкових явищ, ґрунтується на вивченні статистичних даних – відомостей про те, які значення прийняла окрема ознака унаслідок проведення досліду. На практиці статистичних досліджень відрізняють два види дослідів: суцільний і вибірковий. Вся сукупність елементів, яку треба вивчити називається генеральною сукупністю. Та частина об’єктів, що її відібрано для безпосереднього вивчення із генеральної сукупності, називається вибірковою сукупністю. Сутність вибіркового методу полягає в тому, щоб за деякою частиною генеральної сукупності робити висновки про її властивості в цілому. Щоб за даними вибірки мати можливість судити про генеральну сукупність, вона повинна бути взята випадково. Розрізняють наступні види вибірок: · власне-випадкова вибірка, отримана випадковим відбором елементів без поділу їх на частини або групи; · механічна вибірка, для якої елементи генеральної сукупності відбираються через деякий інтервал; · типова вибірка, у яку випадковим чином вибираються елементи з типових груп, на які за деякою ознакою поділяється генеральна сукупність; · серійна вибірка, у яку випадковим чином потрапляють не елементи груп, а власне групи, які потім суцільно досліджуються. _________________________________
53. Емпірична функція розподілу. Нехай відомий статистичний розподіл частот кількісної ознаки Х. Позначимо: пх – число спостережень, при яких спостерігалося значення ознаки, менше х; п – об'єм вибірки. Відносна частота події Х < х дорівнює пх/п. Якщо х змінюється, то змінюється й відносна частота, тобто відносна частота є функція від х. Оскільки ця функція знаходиться емпіричним шляхом, то її називають емпіричною. Емпіричною функцією розподілу називають функцію F*(х), яка визначає для кожного значення х відносну частоту події Х < х. F*(х) = пх / п, де пх - число варіант, менших х; п – об'єм вибірки. Властивості емпіричної функції розподілу: 1) значення емпіричної функції розподілу належать відрізку [0,1]; 2) F*(х) – неспадна функція; 3) якщо х1 – найменша варіанта, то F*(х) = 0 при х < х1; якщо хк – найбільша варіанта, то F*(х) = 1 при х > хк. Емпірична функція розподілу вибірки служить для оцінки теоретичної функції розподілу генеральної сукупності. _________________________________ 54. Статистичні оцінки параметрів генеральної сукупності. Статистичні гіпотези. Інформація, яку дістали на основі обробки вибірки про ознаку генеральної сукупності, завжди міститиме певні похибки, оскільки вибірка становить лише незначну частину від неї, тобто обсяг вибірки значно менший від обсягу генеральної сукупності. Тому слід організувати вибірку так, щоб ця інформація була найбільш повною (вибірка має бути репрезентативною) і забезпечувала з найбільшим ступенем довіри про параметри генеральної сукупності або закон розподілу її ознаки. Параметри генеральної сукупності M(xi)=Xг, Dг, δг, Mo, rxy є величинами сталими, але їх числове значення невідоме. Ці параметри оцінюються параметрами вибірки: Тут через θ позначено оцінювальний параметр генеральної сукупності, а через _________________________________
55. Точкові статистичні оцінки. Статистична оцінка _________________________________
56. Інтервальні статистичні оцінки. Точкова статистична оцінка називається ґрунтовною, якщо у разі необмеженого збільшення обсягу вибірки _________________________________
57. Нульова й альтернативна гіпотези. Гіпотезу, що підлягає перевірці, називають основною. Оскільки ця гіпотеза припускає відсутність систематичних розбіжностей (нульові розбіжності) між невідомим параметром генеральної сукупності і величиною, що одержана внаслідок обробки вибірки, то її називають нульовою гіпотезою і позначають Н0. Зміст нульової гіпотези записується так:
Кожній нульовій гіпотезі можна протиставити кілька альтернативних (конкуруючих) гіпотез, які позначають символом Нa, що заперечують твердження нульової. _________________________________
58. Область прийняття гіпотези. Критична область. Для перевірки правильності висунутої статистичної гіпотези вибирають так званий статистичний критерій, керуючись яким відхиляють або не відхиляють нульову гіпотезу. Статистичний критерій, котрий умовно позначають через K, є випадковою величиною, закон розподілу ймовірностей якої нам заздалегідь відомий. Спостережуване значення критерію, який позначають через K*, обчислюють за результатом вибірки. Сукупність значень статистичного критерію K Î А, за яких нульова гіпотеза не відхиляється, називають областю прийняття нульової гіпотези. Сукупність значень статистичного критерію K Î Якщо при Якщо ж при _________________________________ 59. Алгоритм перевірки правильності нульової гіпотези. Для перевірки правильності Н0 задається так званий рівень значущості a. a — це мала ймовірність, якою наперед задаються. Вона може набувати значення a = 0,005; 0,01; 0,001. Алгоритм перевірки правильності Н0: 1. Сформулювати Н0 й одночасно альтернативну гіпотезу Нa. 2. Вибрати статистичний критерій, який відповідав би сформульованій нульовій гіпотезі. 3. Залежно від змісту нульової та альтернативної гіпотез будується правобічна, лівобічна або двобічна критична область. 4. Для побудови критичної області необхідно знайти критичні точки. За вибраним статистичним критерієм та рівнем значущості a знаходяться критичні точки. 5. За результатами вибірки обчислюється спостережуване значення критерію 6. Відхиляють чи приймають нульову гіпотезу. _________________________________
|


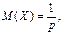

 попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.
попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями. то ця сума має розподіл
то ця сума має розподіл 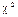 з
з  ступенями волі. Щільність розподілу
ступенями волі. Щільність розподілу


 - Ф
- Ф 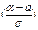 ,
,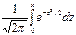 - функція Лапласа.
- функція Лапласа.


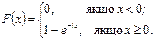
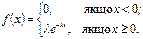
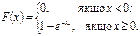
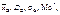
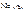 які дістають при обробці вибірки. Вони є величинами непередбачуваними, тобто випадковими.
які дістають при обробці вибірки. Вони є величинами непередбачуваними, тобто випадковими.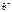 — його статистичну оцінку, яку називають ще статистикою. При цьому θ = const, а
— його статистичну оцінку, яку називають ще статистикою. При цьому θ = const, а  — випадкова величина, що має певний закон розподілу ймовірностей. Зауважимо, що до реалізації вибірки кожну її варіанту розглядають як випадкову величину, що має закон розподілу ймовірностей ознаки генеральної сукупності з відповідними числовими характеристиками: M(xi)=Xг=M(x), D(xi)=Dг, δ(xi)=δг
— випадкова величина, що має певний закон розподілу ймовірностей. Зауважимо, що до реалізації вибірки кожну її варіанту розглядають як випадкову величину, що має закон розподілу ймовірностей ознаки генеральної сукупності з відповідними числовими характеристиками: M(xi)=Xг=M(x), D(xi)=Dг, δ(xi)=δг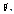 яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що
яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що  то
то  називається незміщеною; в противному разі, тобто коли
називається незміщеною; в противному разі, тобто коли  точкова статистична оцінка
точкова статистична оцінка  (3) називається зміщенням статистичної оцінки
(3) називається зміщенням статистичної оцінки 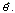 Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка
Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка 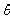 наближається до оцінювального параметра θ, а саме:
наближається до оцінювального параметра θ, а саме:  Точкові статистичні оцінки
Точкові статистичні оцінки  є випадковими величинами, а тому наближена заміна θ на
є випадковими величинами, а тому наближена заміна θ на 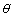 часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою
часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою  та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме:
та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме:  (04) де δ є точністю оцінки. Оскільки
(04) де δ є точністю оцінки. Оскільки 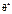 є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. Імовірність, з якою береться нерівність (04), тобто
є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. Імовірність, з якою береться нерівність (04), тобто  , (05) називають надійністю. Рівність (05) можна записати так:
, (05) називають надійністю. Рівність (05) можна записати так: 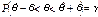 . Інтервал
. Інтервал  , що покриває оцінюваний параметр θ генеральної сукупності з заданою надійністю g, називають довірчим.
, що покриває оцінюваний параметр θ генеральної сукупності з заданою надійністю g, називають довірчим.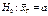 ;
;  ;
;  .
. , за яких нульова гіпотеза не приймається, називають критичною областю. Отже, А — область прийняття Н0,
, за яких нульова гіпотеза не приймається, називають критичною областю. Отже, А — область прийняття Н0, 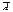 — критична область, де Н0 відхиляється. Точку або кілька точок, що поділяють множину W на підмножини А і
— критична область, де Н0 відхиляється. Точку або кілька точок, що поділяють множину W на підмножини А і 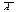 , називають критичними і позначають через Kкр. Існують три види критичних областей: Якщо при K < Kкр нульова гіпотеза відхиляється, то в цьому разі ми маємо лівобічну критичну область, яку умовно можна зобразити.
, називають критичними і позначають через Kкр. Існують три види критичних областей: Якщо при K < Kкр нульова гіпотеза відхиляється, то в цьому разі ми маємо лівобічну критичну область, яку умовно можна зобразити.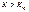 нульова гіпотеза відхиляється, то в цьому разі маємо правобічну критичнуобласть
нульова гіпотеза відхиляється, то в цьому разі маємо правобічну критичнуобласть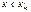 і при
і при  нульова гіпотеза відхиляється, то маємо двобічну критичнуобласть.
нульова гіпотеза відхиляється, то маємо двобічну критичнуобласть.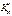 .
.


