И качеством питьевой воды в городе М.
1. Найдем 2. Определим отклонения каждого члена в каждом ряду от их средних значений ( 3. Заполним графы 6-8 табл. 23 с учетом знаков. 4. Полученные значения подставим в формулу для расчета коэффициента линейной корреляции. В нашем примере
5. По таблице (см. приложение 4) определим достоверность коэффициента корреляции. В нашем примере число степеней свободы n=7, критическая величина «rху» при вероятности ошибки 5% = 0,666. Следовательно, коэффициент корреляции достоверен. Если он достоверен, по таблице (см. табл. 22) определим силу связи. В приведенном примере имеет место сильная прямая связь между заболеваемостью вирусным гепатитом А и качеством питьевой воды из поверхностных водоисточников в городе М. Метод корреляции рангов (Спирмена) Этот наиболее простой, но менее точный способ измерения корреляции между признаками относится к непараметрическим методам статистического изучения связи. Он применяется при относительно большом числе наблюдений, при отсутствии точного количественного значения признаков, при нелинейных связях между явлениями, но не используется при прямом и обратном синхронном изменении признаков, что в эпидемиологии встречается редко. При использовании коэффициента корреляции рангов анализируют не показатели, а их условные ранги. Коэффициент корреляции рангов (r – «ро») рассчитывается по формуле: Где d – модуль разности рангов заболеваемости и признака, влияние которого на заболеваемость изучается, n – число наблюдений. Достоверность коэффициента корреляции рангов определяется по специальной таблице «Критические значения коэффициента корреляции рангов» (приложение 5), либо аналогично коэффициенту линейной корреляции по отношению коэффициента к своей ошибке:
Рассмотрим пример влияния среднемесячной температуры воздуха в летние месяцы на среднемесячную заболеваемость вирусным гепатитом А. Для этого ранжируем динамические ряды в порядке возрастания, заполняем таблицу (см. табл. 24). В данном примере температура воздуха на протяжении 3-х лет (2, 3, 4) имела одинаковое значение (16,0). Особенности ранжирования при наличии равных вариант следующие: равным значениям присваивается одинаковый номер ранга, являющийся среднеарифметическим мест, занимаемых данными значениями (ранг =(1+2+3)/3=2). Далее рассчитываем коэффициент корреляции Спирмена и определяем его достоверность по «t» критерию Стъюдента:
Таблица 24 Влияние среднемесячной температуры воздуха в теплое время года на среднемесячную заболеваемость вирусным гепатитом А в городе Б.
В нашем примере число степеней свободы n’=5 (7-2), величина «t» при вероятности ошибки 5% = 2,571, а критическое значение коэффициент корреляции Спирмена =0,94. Следовательно, установленная сильная прямая связь между заболеваемостью вирусным гепатитом А и среднемесячной температурой недостоверна. При любом сравнении, если критерий оценки не достигает заданного уровня статистической значимости, делают вывод о том, что наблюдавшееся соотношение – малонадежный критерий для каких-либо выводов. При малом числе наблюдений можно говорить о достоверности только сильных связей. Методы определения связей между воздействием и следствием (заболеваемостью) В эпидемиологических исследованиях часто приходится сравнивать явления, связанные со здоровьем в двух группах населения, одна из которых представляет группу вмешательства (опытную группу), а вторая – группу контроля. Группа вмешательства – это группа населения, которая подвергалась определенному медицинскому воздействию (вакцинация, экстренная профилактика, изоляция и т.п.) и в этом случае определяют его эффективность в сравнении с группой контроля, которая подобному воздействию не подвергалась. Группой вмешательства также может быть группа населения, которая подвергалась воздействию какого-либо потенциального фактора риска (природного или социального характера), действие которого могло привести к изменениям в состоянии здоровья. В данном случае определяют причинно-следственную связь между влиянием фактора риска (причиной) и изменениями в состоянии здоровья (следствием). Степень связи между воздействием и следствием можно определить с помощью таблицы четырех полей и вычисления ряда коэффициентов (ассоциации, относительного риска, соотношения вероятностей, c2 (хи-квадрат).
|



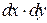
 и
и 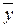 (среднеарифметические значения для рядов х и y).
(среднеарифметические значения для рядов х и y).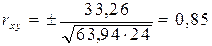 .
. ,
, , где
, где  при n <100 или
при n <100 или 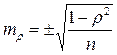 при n > 100.
при n > 100. ;
; ;
; .
.


