Метод линейной корреляции
Коэффициент линейной корреляции используется при небольшом числе (n<;30) несгруппированных наблюдений для оценки прямолинейной связи между двумя явлениями. В основе его вычисления лежит определение отклонений показателей анализируемых рядов от средних арифметических каждого из них с помощью формулы:
где rxy – коэффициент корреляции; dy и dx – отклонения каждой величины от средней арифметической ряда. Достоверность коэффициента корреляции можно оценивать с помощью критерия «t» Стъюдента:
где mr – ошибка коэффициента корреляции, или
Если полученное значение «t» больше табличного (приложение 6) для выбранного уровня доверия и числа степеней свободы, то коэффициент корреляции считается достоверным. Оценить достоверность «r» можно с помощью таблицы «Критические значения коэффициента корреляции» (приложение 4), не прибегая к вычислениям. В этом случае значения полученного коэффициента корреляции сопоставляются с критическим значением для данного числа степеней свободы (n=n-2) и заданного (необходимого) уровня доверия. Полученное значение коэффициента считается достоверным, если оно превышает критическое. Рассмотрим последовательность вычисления коэффициента корреляции на следующем примере. Допустим, по коли-индексу необходимо определить, влияет ли на заболеваемость вирусным гепатитом А качество питьевой воды из поверхностных водоисточников. С этой целью заполним аналитическую таблицу (табл. 23), выполнив следующие расчеты. Таблица 23
|

 ;
;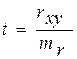 ,
,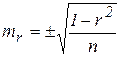 , при числе наблюдений > 100;
, при числе наблюдений > 100;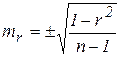 - <100;
- <100; - <30.
- <30.


