Модель А
Распределить по рейсам в два аэропорта назначения имеющиеся в наличии ВС трех типов, обеспечив заданную потребность в пассажирских перевозках при минимальной суммарной себестоимости всех транспортных операций. Осуществим проверку условия совершения транспортной операции при максимальном пассажиропотоке имеющимся парком ВС:
214·2 + 78·6 + 164·4 = 1552 ³ 6655 / 12 + 3652 / 12 = 858.92 – условие выполняется. Целевая функция записывается следующим образом: С = + 1461.055 X21 + 907.352 X22 + 1462.137 X23 ® min.
Ограничения на максимальное количество используемых ВС j-го типа:
X11 / 12 + X21 / 12 £ 2, X12 / 18 + X22 / 12 £ 5, X13 / 12 + X23 / 12 £ 3.
Ограничения на требуемое общее количество перевозимых пассажиров:
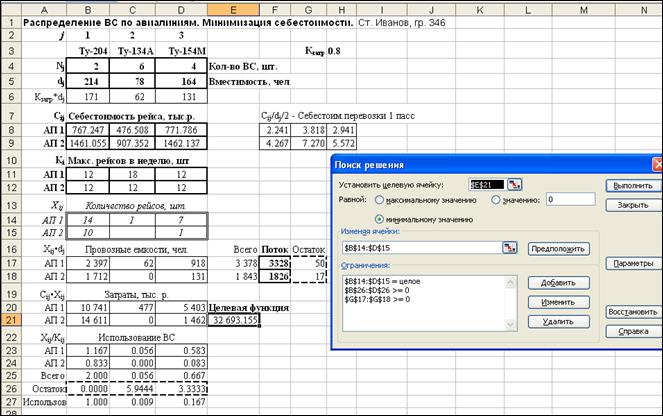
Задача целочисленного линейного программирования решается методом ветвей и границ для различных вариантов распределения пассажиропотока и различных значений коэффициента занятости кресел g. Варианты 1 и 2. Ограничения на требуемое общее количество перевозимых пассажиров записывается следующим образом: g = 1.0 214 X11 + 78 X12 + 164 X13 ³ 6655, 214 X21 + 78 X22 + 164 X23 ³ 3652; g = 0.8 171 X11 + 62 X12 + 131 X13 ³ 6655, 171 X21 + 62 X22 + 131 X23 ³ 3652; g = 0.6 128 X11 + 47 X12 + 98 X13 ³ 6655, 128 X21 + 47 X22 + 98 X23 ³ 3652. Вариант 3. Ограничения на требуемое общее количество перевозимых пассажиров записывается следующим образом: g = 1.0 214 X11 + 78 X12 + 164 X13 ³ 3328, 214 X21 + 78 X22 + 164 X23 ³ 1826; g = 0.8 171 X11 + 62 X12 + 131 X13 ³ 3328, 171 X21 + 62 X22 + 131 X23 ³ 1826; g = 0.6 128 X11 + 47 X12 + 98 X13 ³ 3328, 128 X21 + 47 X22 + 98 X23 ³ 1826. На рисунке 1 представлен вид таблицы MS Excel. Полученные результаты приведены в таблицах 17 и 18.
Распределение ВС по рейсам в вариантах 1 и 2 не отличаются друг от друга, поскольку максимальные значения пассажиропотоков одинаковы. Суммарная себестоимость отличается из-за разницы в затратах на обслуживание пассажиров на рейсах «туда» и рейсах «обратно».
Рисунок 1 – Вид таблицы MS Excel решения задачи (модель А) Распределить по рейсам в два аэропорта назначения имеющиеся в наличии ВС трех типов, обеспечив максимальную суммарную прибыль от выполнения всех транспортных операций. Целевая функция (суммарная прибыль) записывается следующим образом: П = Y1¢ (3.911 - 0.179) + Y2¢ (7.492 - 0.205) + Y1¢¢ (3.911 - 0.204) + Y2¢¢ (7.492 - 0.427) - - (767.247 X11 + 476.508 X12 + 771.786 X13 + 1461.055 X21 + 907.352 X22 + + 1462.137 X23) = = 3.732 Y1¢ + 7.287 Y2¢ + 3.707 Y1¢¢ + 7.065 Y2¢¢ - - (767.247 X11 + 476.508 X12 + 771.786 X13 + 1461.055 X21 + 907.352 X22 + + 1462.137 X23) ® max.
Ограничения на максимальное количество используемых ВС j-го типа:
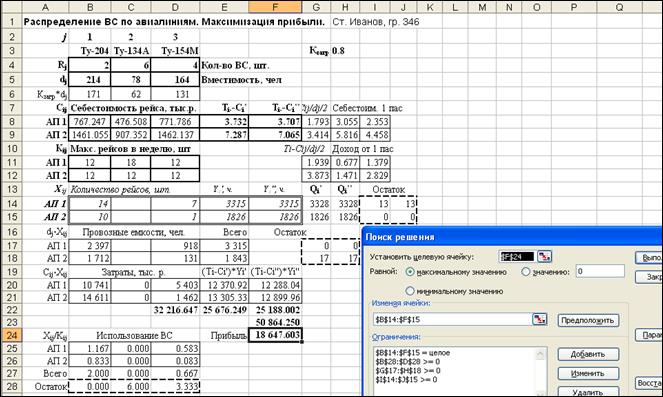
X11 / 12 + X21 / 12 £ 2, X12 / 18 + X22 / 12 £ 5, X13 / 12 + X23 / 12 £ 3. Ограничения на возможное общее количество перевозимых пассажиров: Y1¢ £ Q1¢, Y1¢¢ £ Q1¢¢, Y2¢ £ Q2¢, Y2¢¢ £ Q2¢¢. Ограничения на пассажировместимость ВС: Y1¢ £ Задача целочисленного линейного программирования решается методом ветвей и границ для различных вариантов пассажиропотока и различных значений коэффициента занятости кресел g. Ограничение на пассажировместимость ВС записываются следующим образом: g = 1.0 Y1¢ £ 214 X11 + 78 X12 + 164 X13, Y1¢¢ £ 214 X11 + 78 X12 + 164 X13, Y2¢ £ 214 X21 + 78 X22 + 164 X23, Y2¢¢ £ 214 X21 + 78 X22 + 164 X23; g = 0.8 Y1¢ £ 171 X11 + 62 X12 + 131 X13, Y1¢¢ £ 171 X11 + 62 X12 + 131 X13, Y2¢ £ 171 X21 + 62 X22 + 131 X23, Y2¢¢ £ 171 X21 + 62 X22 + 131 X23; g = 0.6 Y1¢ £ 128 X11 + 47 X12 + 98 X13, Y1¢¢ £ 128 X11 + 47 X12 + 98 X13, Y2¢ £ 128 X21 + 47 X22 + 98 X23, Y2¢¢ £ 128 X21 + 47 X22 + 98 X23. Ограничения на возможное общее количество перевозимых пассажиров записываются следующим образом: Вариант 1: Y1¢ £ 6655, Y1¢¢ £ 0, Y2¢ £ 3652, Y2¢¢ £ 0; Вариант 2: Y1¢ £ 0, Y1¢¢ £ 6655, Y2¢ £ 0, Y2¢¢ £ 3652; Вариант 3: Y1¢ £ 3328, Y1¢¢ £ 3328, Y2¢ £ 1826, Y2¢¢ £ 1826. Полученные результаты приведены в таблицах 19 и 20. На рисунке 2 представлен вид таблицы MS Excel.
Рисунок 2 – Вид таблицы MS Excel решения задачи (модель Б)
\
|

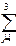 Pj Nj ³
Pj Nj ³ 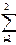 Qi / Mi,
Qi / Mi,