Записать уравнение бюджетной линии, определить ее наклон. Построить бюджетную линию в случаях предоставления субсидий покупателю. Определить оптимальный выбор потребителя в случае двух товаров. Использовать функцию Лагранжа для нахождения необходимого и достаточного условия оптимального положения потребителя в экономике.
1.На доход 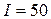 руб. потребитель приобретает два товара по ценам
руб. потребитель приобретает два товара по ценам  и
и 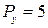 руб. Записать уравнение бюджетной линии, определить ее наклон. Как изменится наклон бюджетной линии, если доход увеличится на 20%, а цены останутся неизменными. Найти новый наклон бюджетной линии, если цена товара
руб. Записать уравнение бюджетной линии, определить ее наклон. Как изменится наклон бюджетной линии, если доход увеличится на 20%, а цены останутся неизменными. Найти новый наклон бюджетной линии, если цена товара  увеличится на 1 руб., а цена товара
увеличится на 1 руб., а цена товара  на 3 руб.
на 3 руб.
2. Функция полезности потребителя 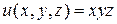 , доход
, доход 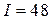 руб., цены товаров
руб., цены товаров  . Найти равновесный набор, имеющий для потребителя максимальную общую полезность.
. Найти равновесный набор, имеющий для потребителя максимальную общую полезность.
3. Функция полезности потребителя  , доход
, доход  руб., цены товаров
руб., цены товаров 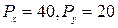 руб. Найти оптимальный набор потребителя, имеющий максимальную общую полезность, используя функцию Лагранжа.
руб. Найти оптимальный набор потребителя, имеющий максимальную общую полезность, используя функцию Лагранжа.
4.Даны три функции полезности потребителя:  ,
, 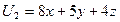 ,
, 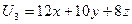 . Весь свой доход
. Весь свой доход  потребитель в каждом случае тратит на покупку трех товаров:
потребитель в каждом случае тратит на покупку трех товаров: 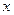 ,
, 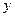 и
и 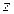 . Цены товаров составляют:
. Цены товаров составляют: 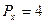 ,
, 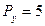 ,
,  . Найдите равновесный набор для каждого случая.
. Найдите равновесный набор для каждого случая.

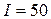 руб. потребитель приобретает два товара по ценам
руб. потребитель приобретает два товара по ценам  и
и 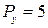 руб. Записать уравнение бюджетной линии, определить ее наклон. Как изменится наклон бюджетной линии, если доход увеличится на 20%, а цены останутся неизменными. Найти новый наклон бюджетной линии, если цена товара
руб. Записать уравнение бюджетной линии, определить ее наклон. Как изменится наклон бюджетной линии, если доход увеличится на 20%, а цены останутся неизменными. Найти новый наклон бюджетной линии, если цена товара  увеличится на 1 руб., а цена товара
увеличится на 1 руб., а цена товара  на 3 руб.
на 3 руб.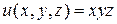 , доход
, доход 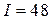 руб., цены товаров
руб., цены товаров  . Найти равновесный набор, имеющий для потребителя максимальную общую полезность.
. Найти равновесный набор, имеющий для потребителя максимальную общую полезность. , доход
, доход  руб., цены товаров
руб., цены товаров 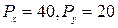 руб. Найти оптимальный набор потребителя, имеющий максимальную общую полезность, используя функцию Лагранжа.
руб. Найти оптимальный набор потребителя, имеющий максимальную общую полезность, используя функцию Лагранжа. ,
, 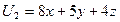 ,
, 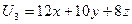 . Весь свой доход
. Весь свой доход  потребитель в каждом случае тратит на покупку трех товаров:
потребитель в каждом случае тратит на покупку трех товаров: 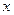 ,
, 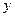 и
и 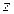 . Цены товаров составляют:
. Цены товаров составляют: 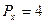 ,
, 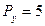 ,
,  . Найдите равновесный набор для каждого случая.
. Найдите равновесный набор для каждого случая.


