Выбор метода совместного анализа.

Базовая модель совместного анализа:

 

 

где U(X) – полная полезность альтернативного варианта;

α_ij – вклад частной ценности или полезности, соответствующей j -му уровню (j = 1, 2, …, k_i) i -го варианта(i = 1, 2, …, m);

k_i – число уровней характеристики i;

m – число характеристик;

x_ij = 1, если j -тый уровень i -й характеристики присутствует;

x_ij = 0 в противном случае.

Важность характеристики I_i определяют через диапазон полезностей α_ij по всем уровням этой характеристики:

I_i = {max(α_ij) – min(α_ij)} для каждого i.

Важность характеристики нормируют для уточнения ее важности относительно других характеристики W_i:

Так что .

Существует несколько методов использования базовой модели. Простейший и самый популярный – регрессионный анализ с фиктивными переменными. В этом случае вычисленные переменные состоят из фиктивных переменных для атрибутивных уровней. Если характеристика имеет k_i уровней, ее кодируют через (k_i - 1)-ю фиктивную переменную. Если получены метрические данные, то рейтинги, выраженные в интервальной шкале, образуют зависимую переменную. Если получены неметрические данные, то значения рангов можно преобразовать в 0 или 1, выполнив попарные сравнения между торговыми марками. В этом случае вычисленные переменные представляют различия в атрибутивных уровнях сравниваемых торговых марок.

Кроме того, исследователь должен решить, на каком уровне проводить анализ – каждого респондента или агрегатном. На индивидуальном уровне данные, полученные от каждого респондента, анализируют отдельно. Если анализ выполняют на агрегатном уровне, то надо разработать процедуру для группирования респондентов. Общий подход состоит в том, чтобы сначала определить функции полезности индивидуального уровня. Затем респондентов объединяют в кластеры, исходя из сходства полезностей. После этого выполняют агрегатный анализ для каждого кластера.
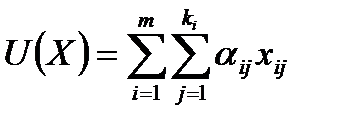