Абсолютная и относительная погрешности. Абсолютной погрешностью измеренияназывается величина, определяемая разницей между результатом измерения х и исходным значением измеряемой величины х0:
Абсолютной погрешностью измерения называется величина, определяемая разницей между результатом измерения х и исходным значением измеряемой величины х0:
Величина
Пример 1. Приближенным значением числа
Значащие цифры. Если абсолютная погрешность величина а не превышает одной единицы разряда последней цифры числа а, то говорят, что у числа все знаки верные. Приближенные числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52 400 равна 100, то это число должно быть записано, например, в виде 524*102 или 0,524*105. Оценить погрешность приближенного числа можно, указав, сколько верно значащих цифр оно содержит. При подсчете значащих цифр не считаются нули с левой стороны числа. Например, число 0,0283 имеет три верных значащих цифры, а 2,5400 – пять верных значащих цифр.
Правила округления чисел. Если приближенное число содержит лишнее (или неверные) знаки, то его следует округлить. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры (d) округленного числа. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если правая отбрасываемая цифра больше или равна d/ 2, то последняя сохраняемая цифра увеличивается на единицу. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются (как и лишние нули). Например, если погрешность измерения 0,001 мм, то результат 1,07005 округляется до 1,070. если первая из измеряемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются. Например, число 148 935 с точностью измерения 50 имеет округление 148 900. Если первая из заменяемых нулями или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или идут нули, то округление производится до ближайшего четного числа. Например, число 123,50 округляется до 124. если первая из изменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя отстающая цифра увеличивается на единицу, например, число 6783,6 округляется до 6784.
Пример 2. При округлении числа 1284 до 1300 абсолютная погрешность составляет 1300 – 1284 = 16, а при округлении 1280 абсолютная погрешность составляет 1280 – 1284 = 4.
Пример 3. При округлении числа 197 до 200 абсолютная погрешность составляет 200 – 197 = 3. Относительная погрешность равна 3/197
Пример 4. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая – 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50/3600
|


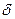 , равная отношению абсолютной погрешности измерения, называется относительной погрешностью:
, равная отношению абсолютной погрешности измерения, называется относительной погрешностью:
 является 3,14. тогда погрешность его равна 0,00159…. абсолютная погрешность можно считать равной 0,0016, а относительную погрешность равной 0,0016/3,14 = 0,00051 = 0,051 %
является 3,14. тогда погрешность его равна 0,00159…. абсолютная погрешность можно считать равной 0,0016, а относительную погрешность равной 0,0016/3,14 = 0,00051 = 0,051 %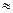 0,01523 или приближенно 3/200
0,01523 или приближенно 3/200 


