Абсолютная и относительная погрешности
Элементы теории погрешностей
Под погрешностью понимается некоторая величина, характеризующая точность результата. Существуют три вида погрешностей: 1) неустранимая погрешность, возникающая из-за неточности исходной информации, например неточности измерений; 2) погрешность метода; 3) погрешность вычислений, возникающая из-за округлений. Основная задача теории погрешностей – указание области неопределенности результата.
Абсолютная и относительная погрешности
Абсолютной погрешностью числа x называется величина D х, удовлетворяющая условию
где x – точное значение величины, а
Отношение абсолютной погрешности к абсолютному значению приближенной величины
называется относительной погрешностью
Относительная погрешность чаще всего указывается в процентах. Точность результата лучше характеризует его относительная погрешность, которая показывает какую часть самого числа составляет погрешность. Абсолютные и относительные погрешности числа принято округлять только в большую сторону, так как при округлениях границы неопределенности числа, как правило, увеличиваются. По этой причине вычисления ведут с одним-двумя запасными знаками. Рассмотрим, как определяются верные значащие цифры чисел. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева. Значащая цифра называется верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре. В противном случае цифра называется сомнительной.
Например, пусть
Если число имеет лишь верные цифры, его округленное значение имеет также лишь верные цифры. Приближенное значение числа, имеющего все верные цифры, может не совпадать с его точным значением. При вычислениях желательно сохранять такое количество значащих цифр, чтобы их число не превышало числа верных цифр более чем на две единицы.
|

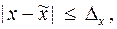
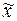 – ее приближенное значение. В этом случае говорят, что
– ее приближенное значение. В этом случае говорят, что 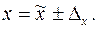

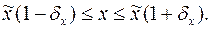
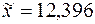 и известно, что
и известно, что 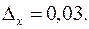 Тогда число
Тогда число