Прямая задача теории погрешностей
Пусть в некоторой области W n-мерного действительного пространства рассматривается непрерывно дифференцируемая функция
z = f(x1, x2,..,xn).
Предположим, что в точке (x1, x2,..,xn) области W нужно вычислить значение Если воспользоваться формулой Лагранжа, то для приближенного значения функции
Рассмотрим распространение погрешностей при выполнении арифметических операций. Пусть x, y – точные значения (x > 0, y > 0), Если
1) При выполнении сложения:
2) При выполнении вычитания:
3) При выполнении умножения:
4) При выполнении деления:
|

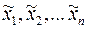 и их погрешности.
и их погрешности. можно получить оценку при малых
можно получить оценку при малых  :
:
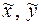 – приближенные значения,
– приближенные значения,  – абсолютные, а
– абсолютные, а  – относительные погрешности значений
– относительные погрешности значений 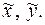
 , тогда
, тогда 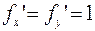 и из (1.3) следует, что
и из (1.3) следует, что  . Приведем формулы определяющие погрешности арифметических операций.
. Приведем формулы определяющие погрешности арифметических операций.






