Указания. а) Входящее в итоговое уравнение время в программе обозначено как переменная с именем tt;
а) Входящее в итоговое уравнение время в программе обозначено как переменная с именем tt; б) Выражаемую уравнением (*) зависимость спроса от времени рассчитать в отдельном столбце; в) Построить на одном рисунке зависимости S(t) и N(t).
Дилеры Проследим динамику развития дилерской сети. Молодые и энергичные дилеры пытаются увеличить спрос на свои товары. Пусть их начальная численность равна D0. Имеется также N0 потенциальных покупателей, которым товар будет продан с какой-то вероятностью. Естественно предположить, что с увеличением количества проданного товара, количество желающих заниматься подобной деятельностью возрастает. В то же время это занятие достаточно хлопотное и постепенно дилеры переходят к другим видам деятельности. Т. е. их численность вследствие естественных причин постоянно уменьшается. Если аналогично порассуждать относительно покупателей, то нетрудно прийти к модели типа «хищник – жертва». При этом дилеры – это «хищники», а покупатели – «жертвы» (если почитать современную прессу, то аналогия полная – к примеру, когда старушкам продают совершенно ненужный им, а иногда и не работающий, очередной китайский прибор «от всех болезней»). Данная модель описывается системой:
где N1 и N2 – текущие количества жертв и хищников; k1, k2, k3, k4 – соответственно коэффициент размножения жертв, вероятность быть съеденным при встрече с хищником (для жертв), вероятность поймать жертву (для хищников), коэффициент смертности (для хищников).
|

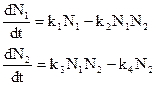 ,
,


