Методы, применяемые после дисперсионного анализа
Дисперсионный анализ показывает – существует ли статистически существенное влияние изучаемого фактора на свойства объекта? Экспериментатора же помимо этого интересует также вопрос – а каково конкретное влияние фактора и как меняются свойства объекта при переходе от одного уровня фактора к другому? Другими словами – экспериментатору важно выяснить – существует ли статистически существенное различие в средних значениях по уровням фактора. Заметим, что в случае фактора с двумя уровнями этот вопрос не стоит. В самом деле, если дисперсионный анализ показал, что имеется статистически существенное влияние фактора, то автоматически существенно различаются и средние по этим двум уровням. А как быть, если число уровней фактора больше двух? Например, в рассмотренном выше примере, экспериментатора может заинтересовать вопрос: а если разница между красками B и D? Для них средние значения вроде бы близки (11,8 и 9,8 соответственно).
Для этих целей наиболее часто используется ранговый критерий Дункана
Общую схему применения этого критерия рассмотрим на вышеприведенном примере. Она состоит из следующих этапов.
1. Упорядочить k средних по возрастанию.
В нашем примере k=4 и упорядоченные средние представляются рядом:
| Средние
| 9,8
| 11,8
| 20,6
| 29,8
| | Тип краски
| D
| B
| A
| C
|
2. Из таблицы дисперсионного анализа берется дисперсия ошибки с соответствующим числом степеней свободы.
В нашем случае: s2e = 8,35 при f = 16.
3. Вычисляется нормированная ошибка для среднего по испытанию:
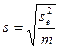 , (7.4) , (7.4)
где m – число опытов в одном варианте испытаний.
В нашем случае:
 . .
4. Из таблицы критерия Дункана выписываются (k-1) рангов при выбранном уровне значимости и числе степеней свободы, соответствующем ошибке.
| F
| Ранг
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| 18,0
| |
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| 6,09
| |
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| 4,50
| |
| 3,93
| 4,01
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| 4,02
| |
| 3,64
| 3,74
| 3,79
| 3,83
| 3,83
| 3,83
| 3,83
| 3,83
| 3,83
| 3,83
| 3,83
| 3,83
| 3,83
| |
| 3,46
| 3,58
| 3,64
| 3,68
| 3,68
| 3,68
| 3,68
| 3,68
| 3,68
| 3,68
| 3,68
| 3,68
| 3,68
| |
| 3,35
| 3,47
| 3,54
| 3,58
| 3,60
| 3,61
| 3,61
| 3,61
| 3,61
| 3,61
| 3,61
| 3,61
| 3,61
| |
| 3,26
| 3,39
| 3,47
| 3,52
| 3,55
| 3,56
| 3,56
| 3,56
| 3,56
| 3,56
| 3,56
| 3,56
| 3,56
| |
| 3,20
| 3,34
| 3,41
| 3,47
| 3,50
| 3,52
| 3,52
| 3,52
| 3,52
| 3,52
| 3,52
| 3,52
| 3,52
| |
| 3,15
| 3,30
| 3,37
| 3,43
| 3,46
| 3,47
| 3,47
| 3,47
| 3,47
| 3,47
| 3,47
| 3,47
| 3,47
| |
| 3,11
| 3,27
| 3,35
| 3,39
| 3,43
| 3,44
| 3,45
| 3,46
| 3,46
| 3,46
| 3,46
| 3,46
| 3,46
| |
| 3,08
| 3,23
| 3,33
| 3,36
| 3,40
| 3,42
| 3,44
| 3,44
| 3,46
| 3,46
| 3,46
| 3,46
| 3,46
| |
| 3,06
| 3,21
| 3,30
| 3,35
| 3,38
| 3,41
| 3,42
| 3,44
| 3,45
| 3,45
| 3,46
| 3,47
| 3,47
| |
| 3,03
| 3,18
| 3,27
| 3,33
| 3,37
| 3,39
| 3,41
| 3,42
| 3,44
| 3,45
| 3,46
| 3,47
| 3,47
| |
| 3,01
| 3,16
| 3,25
| 3,31
| 3,36
| 3,38
| 3,40
| 3,42
| 3,43
| 3,44
| 3,45
| 3,46
| 3,47
| |
| 3,00
| 3,15
| 3,23
| 3,30
| 3,34
| 3,37
| 3,39
| 3,41
| 3,43
| 3,44
| 3,45
| 3,46
| 3,47
| |
| 2,98
| 3,13
| 3,22
| 3,28
| 3,33
| 3,36
| 3,38
| 3,40
| 3,42
| 3,44
| 3,45
| 3,46
| 3,47
| |
| 2,97
| 3,12
| 3,21
| 3,27
| 3,32
| 3,35
| 3,37
| 3,39
| 3,41
| 3,43
| 3,45
| 3,46
| 3,47
| |
| 2,96
| 3,11
| 3,19
| 3,26
| 3,31
| 3,35
| 3,37
| 3,39
| 3,41
| 3,43
| 3,44
| 3,46
| 3,47
| |
| 2,95
| 3,10
| 3,18
| 3,25
| 3,30
| 3,34
| 3,36
| 3,38
| 3,40
| 3,43
| 3,44
| 3,46
| 3,47
| |
| 2,93
| 3,08
| 3,17
| 3,24
| 3,29
| 3,32
| 3,35
| 3,37
| 3,39
| 3,42
| 3,44
| 3,45
| 3,46
| | …
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 2,80
| 2,95
| 3,05
| 3,12
| 3,18
| 3,22
| 3,26
| 3,29
| 3,32
| 3,36
| 3,40
| 3,42
| 3,45
| | …
|
|
|
|
|
|
|
|
|
|
|
|
|
| | ∞
| 2,77
| 2,92
| 3,02
| 3,09
| 3,15
| 3,19
| 3,23
| 3,26
| 3,29
| 3,34
| 3,38
| 3,41
| 3,44
| | | | | | | | | | | | | | | | |
В нашем примере для f = 16 и  =0,05 выписанные ранги выглядят следующим образом: =0,05 выписанные ранги выглядят следующим образом:
5. Получить наименьшие значимые ранги путем умножения выписанных рангов на нормированную ошибку.
В нашем случае:
6. Произвести сравнение наблюдаемых разностей между средними с вычисленными НЗР по схеме:
разница между рядом стоящими средними сравнивается с минимальным НЗР (при № = 2);
разница между средними через одно сравнивается с НЗР при № = 3;
разница между средними через два сравнивается с НЗР при № = 4 и т. д.
Если НЗР больше наблюдаемых разностей, то сравниваемые средние отличаются несущественно. Иначе различие между средними признается статистически значимым.
В нашем случае:
1) 11,8 – 9,8 = 2 <3,876
2) 20,6 – 9,8 = 10,8 > 4,070
3) 29,8 – 9,8 = 20 > 4,173
4) 20,6 – 11,8 = 8,8 >3,876
5) 29,8 – 11,8 = 18 > 4,070
6) 29,8 – 20,6 = 9,2 > 3,876
В результате сравнения обнаружено, что первое и второе среднее отличаются несущественно, а разница между остальными средними статистически значима.
Результаты сравнения можно наглядно представить на одномерной шкале.
D B A C
9,8 11,8 20,6 29,8
Здесь средние, отличающиеся несущественно, имеют одну общую черту.
Таким образом по результатам испытаний защитных красок можно сказать следующее:
краски D и B обладают наилучшими защитными свойствами и примерно одинаковы. Наихудшими защитными свойствами обладает краска C. Краска А является промежуточной по защитным свойствам.
Варианты заданий
Варианты заданий взять из Приложения 2 «Районы и города Чувашии в цифрах».
Во всех заданиях методом дисперсионного анализа выяснить имеется ли различие в средних значениях показателя по уровням изучаемого фактора и дать экономическую интерпретацию полученных результатов.

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
Кишечный шов (Ламбера, Альберта, Шмидена, Матешука) Кишечный шов– это способ соединения кишечной стенки.
В основе кишечного шва лежит принцип футлярного строения кишечной стенки...
Принципы резекции желудка по типу Бильрот 1, Бильрот 2; операция Гофмейстера-Финстерера. Гастрэктомия Резекция желудка – удаление части желудка:
а) дистальная – удаляют 2/3 желудка б) проксимальная – удаляют 95% желудка. Показания...
|
КОНСТРУКЦИЯ КОЛЕСНОЙ ПАРЫ ВАГОНА Тип колёсной пары определяется типом оси и диаметром колес. Согласно ГОСТ 4835-2006* устанавливаются типы колесных пар для грузовых вагонов с осями РУ1Ш и РВ2Ш и колесами диаметром по кругу катания 957 мм. Номинальный диаметр колеса – 950 мм...
Философские школы эпохи эллинизма (неоплатонизм, эпикуреизм, стоицизм, скептицизм). Эпоха эллинизма со времени походов Александра Македонского, в результате которых была образована гигантская империя от Индии на востоке до Греции и Македонии на западе...
Демографияда "Демографиялық жарылыс" дегеніміз не? Демография (грекше демос — халық) — халықтың құрылымын...
|
|

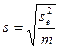 , (7.4)
, (7.4) .
. =0,05 выписанные ранги выглядят следующим образом:
=0,05 выписанные ранги выглядят следующим образом:



