Использование уравнения для прогноза
Для прогноза достаточно скопировать данные и формулы на нужное значение Х. В данном случае:
Таким образом, прогнозируемое значение Y на X=3,1 равно 1,97. Для оценки точности прогноза сначала рассчитывается стандартное отклонение в точке прогноза:
где n – число измерений; xp – значение x, для которого осуществляется прогноз;
Суммирование в формуле производится по имеющимся значениям y. Далее рассчитывается доверительный интервал прогноза – dy:
где tтабл – табличное значение критерия Стьюдента при выбранном уровне значимости и числе степеней свободы, равном n-1. Результирующий прогноз имеет вид:
Непосредственно для расчетов: – в D19 вычислить среднее X =СРЗНАЧ(C7:C16); – в D20 вычислить общую дисперсию для Х =ДИСПА(C7:C16)*9; – в D21 вычислить общую дисперсию для реальных данных =ДИСПА(E7:E16)*9; – в D22 вычислить остаточную дисперсию для уравнения прогноза =СУММКВРАЗН(E7:E16;G7:G16); – в D23 вычислить стандартное отклонение для Y =(D22/8)^(1/2); – в D24 вычислить точность прогноза =D23*(1+1/10+(3,1-D19)^2/D20)^(1/2); – в D25 вычислить критерий Стьюдента =СТЬЮДРАСПОБР(0,05;9), где 0,05 – уровень значимости предсказания, что соответствует надежности 1 – 0,05 = 0,95 (95%); 9 – количество реальных данных минус 1. – в D26 вычислить доверительный интервал =D25*D24.
В результате должно получиться следующее:
Таким образом, прогнозируемое значение равно: 1,97± 4,97.
|

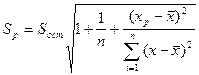 , (7.14)
, (7.14)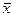 – среднее значение x, для имеющихся данных;
– среднее значение x, для имеющихся данных; – стандартное отклонение остаточной суммы квадратов, рассчитываемое по формуле:
– стандартное отклонение остаточной суммы квадратов, рассчитываемое по формуле: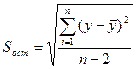 . (7.15)
. (7.15) , (7.16)
, (7.16)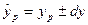 . (7.17)
. (7.17)


