Порядок выполнения работы. 1. Взять данные своего варианта из Приложения 4«Транспорт и связь» или открыть файл Транспорт и связь.doc.

1. Взять данные своего варианта из Приложения 4 «Транспорт и связь» или открыть файл Транспорт и связь.doc.

2. Скопировать данные своего варианта в новую рабочую книгу. Пусть это будут следующие данные:

 

Y (показатель)	X (время)
	0,1
	0,4
	0,7
	1,3
	1,6
	1,9
	2,2
	2,5
	2,8

3. Последовательно рассчитать столбцы значений X², X³ и X⁴.

 

	A	B	C	D	E
	Y	X	X2	X3	X4
		0,1	0,01	0,001	0,0001
		0,4	0,16	0,064	0,0256
		0,7	0,49	0,343	0,2401
		1,3	1,69	2,197	2,8561
		1,6	2,56	4,096	6,5536
		1,9	3,61	6,859	13,0321
		2,2	4,84	10,648	23,4256
		2,5	6,25	15,625	39,0625
		2,8	7,84	21,952	61,4656

 

4. В строке 13 получить уравнение регрессии первой степени. Для этого в B13 вызывается функция ЛИНЕЙН и в качестве ее аргументов указывается:

известные значения Y – A2:A11;

известные значения X – B2:B11.

В результате выполнения функции в B13 появится число, соответствующее коэффициенту а₁ в уравнении (1). Для того, чтобы увидеть второй коэффициент необходимо выделить ячейки B13:C13, затем нажать F2 и затем выполнить тройное нажатие Ctrl+Shift+Enter.

Для обрабатываемых данных получатся следующие значения:

 

	A	B	C
	Y1=	0,707071	6,274747

 

5. В строке 14 получить уравнение регрессии второй степени. Для этого в B14 вызывается функция ЛИНЕЙН и в качестве ее аргументов указывается:

известные значения Y – A2:A11;

известные значения X – B2:С11.

В результате выполнения функции в B14 появится число, соответствующее коэффициенту а₂ в уравнении (2). Для того, чтобы увидеть остальные коэффициенты необходимо выделить ячейки В14:C14, затем нажать F2 и затем выполнить тройное нажатие Ctrl+Shift+Enter.

Для обрабатываемых данных получатся следующие значения:

 

	A	B	C	D
	Y2=	-3,28283	10,22727	1,810101

 

6. Аналогично в строках 15 и 16 получить коэффициенты полиномов 3 и 4-ой степени.

7. Используя полученные уравнения регрессии рассчитать предсказываемые с его помощью значения выходного параметра.

Пример расчета по уравнению первой степени:

В G2 вводится формула =$C$13+$B$13*B2, которая затем копируется на весь столбец G. При этом должны получиться следующие значения:

 

	A	B	C	D	E	F	G
	Y	X	X2	X3	X4		Y1
		0,1	0,01	0,001	0,0001		6,345455
		0,4	0,16	0,064	0,0256		6,557576
		0,7	0,49	0,343	0,2401		6,769697
							6,981818
		1,3	1,69	2,197	2,8561		7,193939
		1,6	2,56	4,096	6,5536		7,406061
		1,9	3,61	6,859	13,0321		7,618182
		2,2	4,84	10,648	23,4256		7,830303
		2,5	6,25	15,625	39,0625		8,042424
		2,8	7,84	21,952	61,4656		8,254545

 

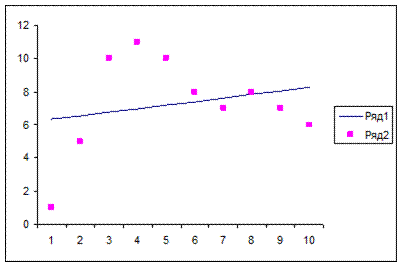
По данным столбцов А и G построить совместный график, общий вид которого показан на рисунке. При этом «экспериментальные» данные (столбец А) представлены точками, а рассчитанные – сплошной линией (рис. 7.1).

 

Рис. 7.1. Результат аппроксимации реальных данных линейной зависимостью

 

И без статистической проверки очевидно, что соответствие между экспериментальными и расчетными данными отсутствует.

В столбцах I, J произвести аналогичные расчеты и построения для полиномов третьей и четвертой степени. При этом при расчетах уравнения третьей степени в качестве параметра известные значения X указать – B2:D11, а уравнения четвертой степени – B2:E11.