Общие сведения. Очень часто данные об экономических объектах представлены в виде последовательностей значений свойств объектов в различные моменты времени
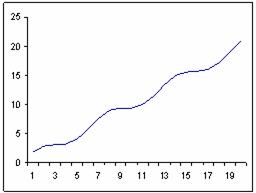
Очень часто данные об экономических объектах представлены в виде последовательностей значений свойств объектов в различные моменты времени. Такая зависимость называется временным рядом. Основная задача обработки временных рядов заключается в выявлении особенностей ряда с целью возможного прогноза свойств объекта в последующие моменты времени. Анализ поведения экономических объектов во времени показывает, что они обладают рядом общих закономерностей. 1. В поведение объекта всегда имеется регулярная составляющая. Она обычно отражает общую тенденцию развития объекта во времени. Например, спрос на нефть имеет устойчивую тенденцию к возрастанию – рис.7.6.
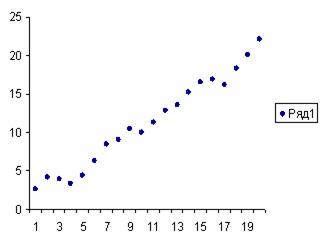
Представленная на рис.7.6 регулярная составляющая представляет собой прямую линию. Но не менее часто встречаются и другие ее виды – рис.7.7.
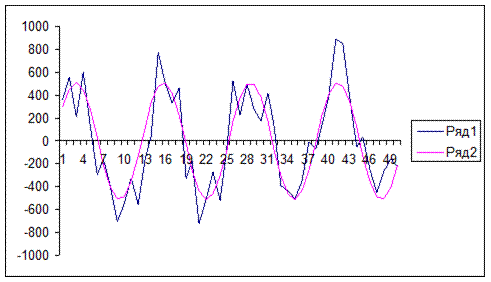
2. На регулярную составляющую накладываются периодические колебания свойств. Эти колебания связаны, как правило, с влиянием времени года на свойства объекта – так называемые сезонные колебания. Например, потребление нефти в зимнее время меньше, чем в летнее. В результате этого, вместо рис.7.6. будет иметь место рис.7.8.
Рис. 7.8. Пример сезонной составляющей
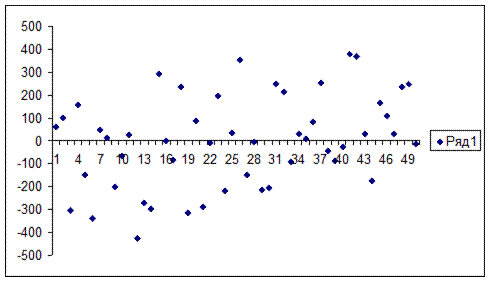
3. К сожалению, временные ряды реальных объектов практически никогда не представляют собой гладкие кривые. Реально они чаще всего имеют вид, представленный на рис.7.9.
Рис. 7.9. Пример наложения случайных возмущений на сезонную составляющую
Вызвано это тем, что на объект влияет слишком большое количество других факторов, часто действующих в противоположном направлении. Эти факторы не столь существенны, как указанные первые два, но их, как правило, во-первых, очень много и, во-вторых, практически невозможно учесть. Поэтому вклад этих факторов рассматривается как случайная составляющая. Применительно к ценам на нефть такими факторами могут быть и стихийные бедствия в районах нефтедобычи, и отдельные заявления руководителей ведущих экономических стран, и попытки скрыть истинные величины потребления, и даже элементарные опечатки при представлении данных.
Основным методом анализа временных рядов экономических данных является метод декомпозиции ряда на указанные составляющие. Пример Суть метода заключается в следующем. 1. Сначала выделяется наиболее существенная регулярная составляющая ряда. Для этого необходимо представить имеющиеся данные в виде графика и хотя бы визуально оценить ее вид. 2. Все множество гладких функций можно описать относительно небольшим набором математических функций. Наиболее простые из них: линейная логарифмическая степенная экспоненциальная Здесь а0, а1, а2 – некоторые числовые коэффициенты. 3. Для всех указанных функций в Excel имеется возможность строить так называемые лини тренда. При выполнении лабораторной работы используется программа Excel «Временные ряды.xls». С помощь кнопки «Генерация» произвести генерацию данных. При этом программа случайным образом выбирает вид регулярной составляющей и выводит полученные данные на лист Excel. Фрагмент данных приведен в таблице.
Скопировать эти данные в новую книгу и на их основе построить диаграмму. Тип диаграммы – график. Для получения линии тренда: Выделить построенную диаграмму – выбрать пункт «Диаграмма» главного меню – Добавить линию тренда – Выбрать тип линии – Через закладку «Параметры» поставить галочку на пункт «Показывать уравнение на диаграмме» - Ok. Если выбран линейный тренд, для представленных данных уравнение имеет вид y=193,87x+234,50. 4. С помощью полученного уравнения рассчитать значение параметра ряда в тех же точках. Для этого в соседнем с данными столбце (D) ввести формулу =193,87*В1+234,5 и скопировать ее на весь столбец. Должно получиться следующее:
5. Получить разность между рассчитанными и имеющимися данными. Для рассматриваемого примера должно получиться следующее:
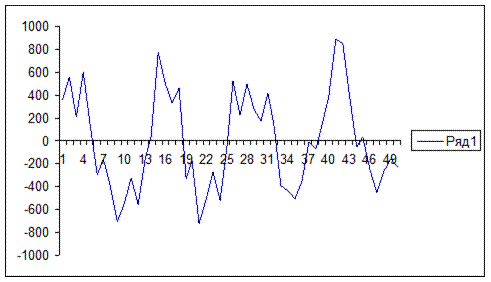
6. По данным столбца Е построить диаграмму остатков (тип диаграммы – график). Для представленных данных получается примерно следующее (рис. 7.10):
Рис. 7.10. Результат удаления из временного ряда регулярной составляющей
7. Оценить качество выбранной линии тренда можно как визуально, так и с помощью суммы остатков. Эта сумма должна быть близкой к нулю. В данном случае она будет равна -0,97. Визуальная оценка состоит в том, что график остатков должен быть похож на искаженную синусоиду. 8. Если полученная диаграмма непохожа на синусоиду (например, большая часть данных смещена относительно оси Х), то это означает, что вид регулярной составляющей выбран неправильно. Поэтому следует повторить этапы 3-7 с трендом другого вида. В некоторых случаях визуальная оценка между конкурирующими трендами затруднена. Поэтому среди них следует выбрать тот, у которого сумма остатков меньше. 9. Выделение остатков завершает выделение регулярной составляющей ряда. Вторым этапом является выделение циклической составляющей ряда. 10. Для этого используется одна из периодических функций – обычно синусоида, уравнение которой в общем виде выглядит следующим образом:
где b0, b1, b3, b3 – некоторые числовые коэффициенты. Коэффициенты отвечают за следующие параметры синусоиды: b0 – за сдвиг синусоиды по оси Y. b1 – за размах значений синусоиды. b3 – за сдвиг синусоиды по оси Х. b3 – за растяжение синусоиды по оси Х.
11. Для определения параметров синусоиды используется встроенное в Excel средство «Поиск решения». 12. Для организации вычислений с его помощью производится следующее: Создается строка коэффициентов, в нее вводятся их начальные значения и по указанному выше уравнению рассчитываются значения остатков. Например:
При этом в столбец F введена формула
=$H$2+$I$2*SIN($J$2+$K$2*B1), которая затем скопирована на весь столбец F.
13. Для нахождения точных значений коэффициентов синусоиды: а) Вычисляется функция СУММКВРАЗН, в качестве аргументов которой указываются столбцы E и F. Пусть это вычисление произведено в ячейке К3 и его начальный результат приведен в предыдущей таблице. б) В ячейки I2, J2 и K2 вводятся примерные значения коэффициентов синусоиды. Их можно оценить следующим образом: b1 – определяет размах синусоиды. Из предыдущего рисунка он примерно равен 600; b2 – определяет сдвиг синусоид по оси Х. Из предыдущего рисунка он, примерно, равен 0; b3 – определяет растяжение синусоиды по оси Х. Из предыдущего рисунка он равен, примерно, 0,5. Эти значения и введены в предыдущую таблицу. в) Курсор устанавливается на ячейку К3 и вызывается средство «Поиск решения». В появившемся окне переключатель установить в положение «Минимальное значение», а в поле «Изменяя ячейки» указать I2:K2 и, затем «Выполнить». Если все было сделано правильно, то для данных чисел получается следующее:
При этом уточнились как сами коэффициенты, так и рассчитанные по ним значения. 14. По данным столбцов E и F построить совместную диаграмму следующего вида (рис. 7.11)
Рис. 7.11. Результат сглаживания сезонной составляющей с помощью формулы (7.18)
Ее внешний вид позволяет визуально оценить качество аппроксимации остатков синусоидой. 15. В столбце G рассчитать остатки второго уровня, т.е. разность между остатками и синусоидой. Для этого в ячейку G1 вводится формула =E1-F1, которая затем копируется на весь столбец. 16. По данным столбца строится диаграмма остатков второго уровня (рис. 7.12).
Рис. 7.12. Диаграмма остатков второго уровня
Если регулярная составляющая была подобрана и рассчитана правильно и, если также правильно была рассчитана периодическая составляющая, то диаграмма должна иметь вид случайного недетерминированного ряда. Признаком случайности является значение суммы этих остатков. Она должна быть много меньшей, чем сумма остатков первого уровня. В данном случае она оказалась равной 0,002332, что намного меньше суммы остатков первого уровня (-0.97).
17. Используя уравнения отдельных составляющих, можно составить общее уравнение ряда. В данном случае оно будет выглядеть следующим образом: y=235,515+193,87*x+510,89*Sin(0,116+0,49*x).
Полученное уравнение можно использовать для целей прогноза. Для этого достаточно подставить в него то значение Х, для которого мы хотим узнать значение Y. Литература 1. Бухвалов, А. В. Финансовые вычисления для профессионалов / А. В. Бухвалов, В. В. Бухвалова, А. В. Идельсон. Под общ. ред. А. В. Бухвалова. – СПб.: БХВ-Петербург, 2001. – 320 с.: ил. 2. Каплан, А. В. Решение экономических задач на компьютере / А. В. Каплан и др. – М.: ДМК Пресс; СПб.: Питер, 2004.- 600 с.: ил. 3. Конрад Карлсберг. Бизнес-анализ с помощью Excel 2000.: Пер. с англ.: уч. пос. – М.: Издательский дом «Вильямс», 2000. – 480 с.: ил. 4. Питер Эйткен. Интенсивный курс программирования в Excel за выходные.: Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 432 с.: ил. 5. Россия в цифрах, 2002: краткий статистический сборник / Гос. ком. Рос. Федерации по статистике (Госкомстат России). – М.: Госкомстат России, 2002. – 399 с. – 5–89476–103–4. 6. Титоренко, Г. А. Автоматизированные информационные технологии в экономике. – М.: Юнити, 2006. – 400 с. 7. Филимонова, Е. В. Информационные технологии в экономике / Филимонова Е. В., Черненко Н. А., Шубин А. С. – М.: Феникс, 2008. – 443 с. 8. Цисарь, И. Ф. Компьютерное моделирование экономики / И. Ф. Цисарь, В. Г. Нейман – М.: «Издательство ДИАЛОГ-МИФИ», 2008. – 384 с. 9. Чувашская Республика и регионы Приволжского федерального округа, 2004: статистический сборник / Ком. гос. статистики Чуваш. Республики. – Чебоксары: Госкомстат Чуваш. Респ., 2004. – 181 с.
|
;
;
;
.
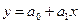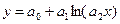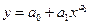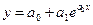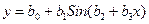, (7.18)
