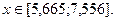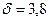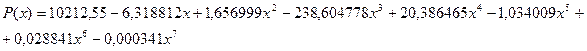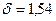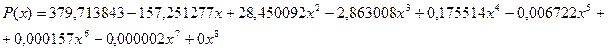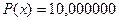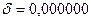Интерполяция функции
Будем находить описывающий функцию полином методом наименьших квадратов. Полином будем строить по всем найденным точкам.
Искомый полином имеет вид
где n – количество контрольных точек. Решение матрицы осуществлялось в программе MathCAD и здесь не приводится ввиду его громоздкости. Отмечу, что в ходе интерполяции было выяснено, что лучше интерполировать функцию по частям. Точки разбиения на отрезки были выбраны таким образом, чтобы значения интерполирующих полиномов слева и справа в данных точках совпадали.
1.
Нули перед коэффициентами означают, что, хотя для интерполяции m было равно 58, коэффициенты перед степенями высоких порядков были равны нулю.
2.
3.
4.
5.
6.
|
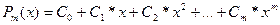, где m – степень полинома. Коэффициенты 
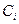находятся из следующей системы уравнений: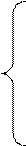
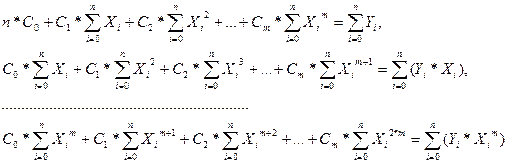
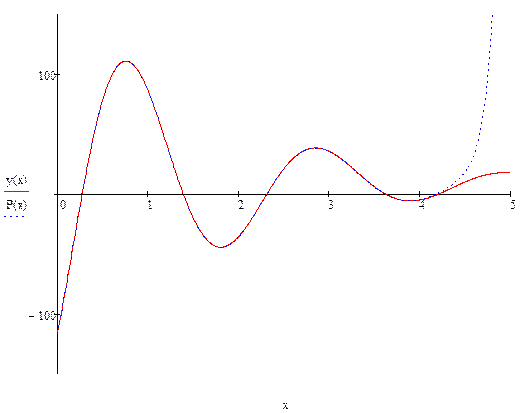
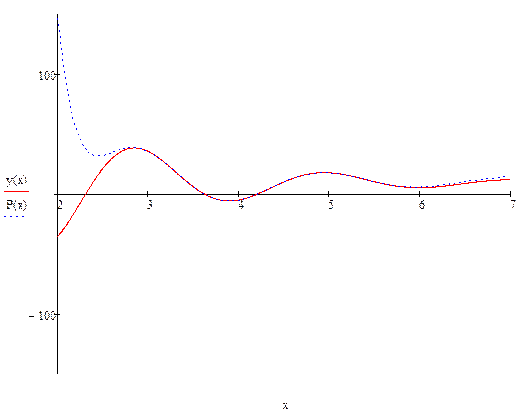
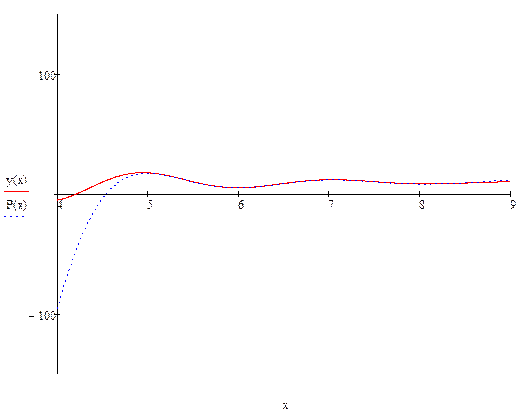
Наилучшим образом функцию на этом отрезке описывает следующий полином:
. Квадратичное отклонение на отрезке по всем точкам 
