Составим математическую модель задачи.
Обозначим через x11+ x12 +x13+ x14 =30 x21+ x22 +x23+ x24 =20 x31+ x32 +x33+ x34 =20 x11+ x21 +x31 =20 (1) x12+ x22 +x32 =20 x13+ x23 +x33=15 x14+ x24 +x34 =15 При данном плане X=(х F=4 x11 + x12 +3 x13 +2 x14 +8 x21 +5 x22 +7 x23 +6 x24 +12 x31 +9 x32 +11 x33 +10 x34 (2) Таким образом, математическая модель данной транспортной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений (1), при котором целевая функция (2) принимает минимальное значение.
1.2. Решение задачи в системе MathCAD.
|
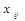количество единиц сырья, перевозимого из i -го пункта его получения на j -е предприятие. Тогда условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:
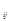)(i = 
; j = 
) перевозок общая стоимость перевозок составит:
