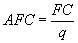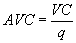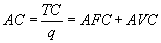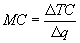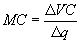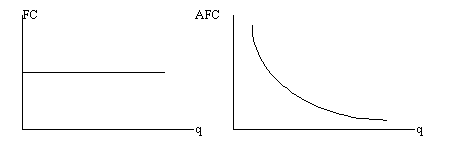ПОСТОЯННЫЕ И ПЕРЕМЕННЫЕ ЗАТРАТЫ
В предыдущем параграфе говорилось, что различие между переменными (VC) и постоянными затратами (FC) состоит в том, что первые меняются при изменении выпуска, а вторые – нет. Сумма постоянных и переменных затрат дает нам совокупные затраты (TC): FC + VC = TC. Помимо совокупных затрат необходимо знать и средние затраты. Средние постоянные затраты (AFC) – это постоянные затраты, приходящиеся на единицу выпуска:
Средние переменные затраты (AVC) – это переменные затраты, приходящиеся на единицу выпуска:
Средние совокупные затраты (AC) – это совокупные затраты, приходящиеся на единицу выпуска или сумма средних постоянных и средних переменных затрат:
При анализе рыночного поведения фирмы большую роль играют предельные затраты. Предельные затраты (MC) отражают прирост суммарных затрат при увеличении выпуска (q) на одну единицу:
Поскольку с ростом выпуска возрастают лишь переменные затраты (D TC = D VC), то можно записать:
Можно сказать и так: предельные затраты – это затраты, связанные с выпуском последней единицы продукции. Приведем пример расчета затрат. Пусть при выпуске 10 ед. переменные затраты составляют 100, а при выпуске 11 ед. они достигают 105. Постоянные затраты не зависят от выпуска и равны 50. Тогда:
В нашем примере выпуск увеличился на 1 ед. (D q = 1), при этом переменные и суммарные затраты возросли на 5 (D VC = D TC = 5). Следовательно, дополнительная единица выпуска потребовала увеличения затрат на 5. Это и есть предельные затраты производства одиннадцатой единицы продукции (МС = 5). Динамику затрат от выпуска можно проиллюстрировать графически, отложив по оси Х выпуск, а по оси Y – затраты. Поскольку постоянные затраты не меняются с ростом выпуска, линия FC идет параллельно оси Х. При этом средние постоянные затраты все время снижаются, т. к. в формуле AFC = FC/q числитель не меняется, а знаменатель растет (рис. 4-1): Рис. 4-1. Кривые постоянных и средних постоянных затрат
Что касается всех остальных затрат, то их графики могут быть разными в зависимости от принятых предпосылок. Упрощенный вариант динамики затрат: Рассмотрим сначала простой вариант динамики затрат, основанный на предпосылке, что предельные затраты постоянны. Такая предпосылка зачастую соответствует практике малого бизнеса. Пусть перед нами небольшой магазин, торгующий пивом. Для торговой фирмы выпуском является количество проданных товаров. Но чтобы продать товар, его надо сначала купить. Соответственно, затраты на закупку пива у оптовика – переменные затраты: чем больше пива продается, тем больше и покупается. Предположим, каждая бутылка закупается по 5 руб. Все остальные затраты (аренду, зарплату продавца и т.д.) полагаем постоянными и составляющими в совокупности 100 руб. в день. Составим таблицу динамики затрат от выпуска – количества проданных бутылок (табл. 4-2): Таблица 4-2. Динамика затрат
В данном случае предельные затраты не меняются вместе с выпуском, поскольку при закупке каждой дополнительной бутылки пива суммарные (переменные) затраты всякий раз возрастают на одну и ту же величину – закупочную цену этой бутылки. Но в таком случае предельные затраты обязательно равны средним переменным затратам, ибо сколько бы бутылок мы не продали переменные затраты на одну бутылку всегда будут равны ее закупочной цене. Это и отражено на рис. 4-2: Рис. 4-2. Предельные и средние переменные затраты
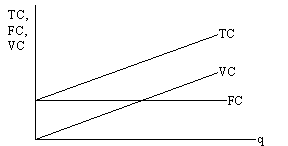
Коль скоро средние переменные затраты не меняются с ростом выпуска, то функции переменных, соответственно и суммарных затрат будут линейны (рис. 4-3): Рис. 4-3. Постоянные, переменные и суммарные затраты
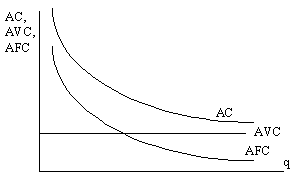
Поскольку TC = FC + VC, а постоянные затраты не меняются, то на рисунке линии переменных и суммарных затрат параллельны друг другу, и расстояние между ними равно постоянным затратам. При нулевом выпуске переменные затраты равны нулю, но постоянные затраты нулю не равны, ибо их приходится нести, даже если фирма ничего не производит. Таким образом, при нулевом выпуске суммарные затраты равны постоянным затратам, т.е. линия ТС выходит из точки постоянных затрат. В связи с этим функции средних затрат будут выглядеть так (рис. 4-4): Рис. 4-4. Средние затраты
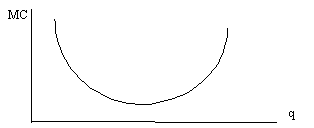
О динамике средних постоянных и средних переменных затрат уже говорилось. Что касается функции средних суммарных затрат (AC), то она убывает и стремится к AVC, поскольку AC = AFC + AVC, причем средние постоянные затраты падают, а средние переменные – остаются прежними. Таким образом, линии AC и AFC параллельны друг другу и расстояние между ними равно AVC. Вывод: чем больше объем выпуска, тем меньше средние постоянные, соответственно и средние суммарные затраты фирмы. Усложненный вариант динамики затрат: Очень часто приходится сталкиваться с усложненным вариантом динамики затрат, основанном на предпосылке, что предельные затраты сначала снижаются, а затем начинают расти (рис. 4-5): Рис. 4-5. Кривая предельных затрат
Это означает, что первоначально каждая следующая единица выпуска требует все меньших дополнительных затрат, а затем тенденция сменяется на противоположную: чем больше выпуск, тем дороже обходится каждая следующая его единица. Приведем условный числовой пример (табл. 4-3): Таблица 4 - 3. Усложненный вариант динамики затрат
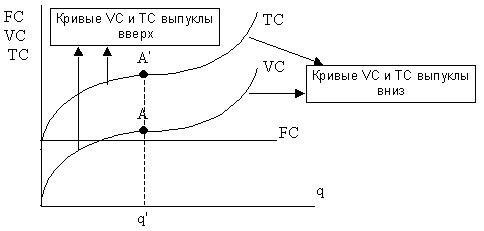
В таком случае функции переменных и суммарных затрат перестают быть линейными, хотя линии TC и VC по-прежнему параллельны друг другу и кривая ТС выходит из точки постоянных затрат (рис. 4-6): Рис. 4-6. Кривые переменных и суммарных затрат
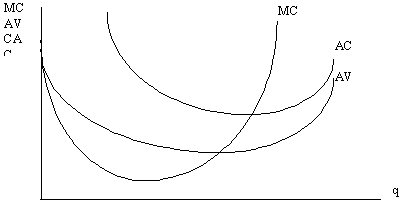
Характер кривых переменных и суммарных затрат обусловлен динамикой предельных затрат. До тех пор, пока предельные затраты убывают, переменные и суммарные затраты возрастают медленнее, нежели выпуск. На рис. 4-6 это отражено выпуклостью кривых VC и TC вверх вплоть до точек перегиба (т. А и А'). При выпуске, соответствующем точкам перегиба (q'), предельные затраты достигают минимума. Затем они начинают возрастать, в результате чего переменные и суммарные затраты увеличиваются быстрее, чем выпуск. Это означает, что кривые VC и TC становятся выпуклыми вниз. Соответственно изменяется и вид кривых средних переменных и средних суммарных затрат (рис. 4-7): Рис. 4-7. Предельные и средние затраты
Функции средних переменных и средних суммарных затрат определяются функцией предельных затрат. Кривые MC и AVC выходят из одной точки: для бесконечно малых величин они равны. Затем предельные затраты снижаются и "тянут за собой" средние переменные затраты, которые тоже падают, но медленнее. При определенном уровне выпуска предельные затраты достигают своего минимума. Далее предельные затраты начинают повышаться, увлекая за собой средние переменные затраты, хотя последние еще некоторое время "по инерции" падают. Дело в том, что средние переменные затраты снижаются до тех пор, пока они больше предельных затрат. Кривая предельных затрат пересекает, следовательно, кривую AVC и в точке ее минимума, после чего обе функции возрастают. Кривая средних суммарных затрат (AC) выходит из бесконечности, поскольку при производстве, близком к нулю, постоянные затраты все равно приходится нести, и, следовательно, суммарные затраты на единицу выпуска очень высоки. Затем средние суммарные затраты падают, достигая минимума в точке пересечения с кривой предельных затрат. Точка минимума средних суммарных затрат находится правее точки минимума средних переменных затрат. Это объясняется тем, что средние суммарные затраты включают в себя не только средние переменные, но и средние постоянные затраты, а последние все время снижаются. По мере повышения выпуска кривые AC и AVC постоянно сближаются, поскольку средние постоянные затраты стремятся к нулю.
|