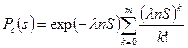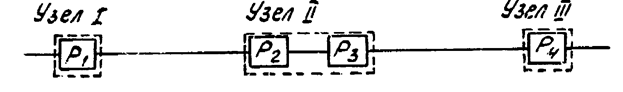РАСЧЕТ БЕЗОТКАЗНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ ПРИ ОСНОВНОМ И РЕЗЕРВНОМ СОЕДИНЕНИЯХ ЭЛЕМЕНТОВ
Расчетные формулы для расчета вероятности безотказной работы технической системы при основном соединении элементов, когда отказ технической системы наступает при отказе одного из элементов, имеют следующий вид:
или Если li=constи время возникновения отказов подчинено экспоненциальному закону распределения. Тогда количественные характеристики безотказности можно представить в виде Pc(t)=exp [-lc t]=exp [- t/Tср], lc= å li, аc(t) = lc exp [-lct], Tср.с = 1/lc(20) Если все элементы рассматриваемого устройства равнонадежны, то
где Ni - число элементов i-го типа; r - число типов элементов. Для высоконадежных систем, для которых lt < 0,1, можно воспользоваться приближенными формулами, разложив ехр [-lct]в ряд и ограничиться первыми двумя членами, тогда
Поскольку
где Qi (t) = 1 - Pi (t)- вероятность отказа i-го элемента. В невосстанавливаемых изделиях с резервным (параллельным) соединением элементов отказ одного из элементов не приводит к отказу системы в целом. Система откажет только тогда, когда откажут все элементы. Поскольку элементы независимы, то вероятность отказа системы
Вероятность безотказной работы системы
Среднее время безотказной работы системы
Пример 2.1. Определить вероятность безотказной работы системы из надежного (P1= 0,9) и ненадежного (P2= 0,4) элементов. 1. При основном соединении элементов
Pc = P1 P2 = 0,9 0,4 = 0,36 2.При резервном соединении элементов
Pc = 1 - [(1-P1) (1-P2)] = 1 - [(1-0,9)(1-0,4)] = 0,94. 3. При резервном соединении двух надежных элементов
Pc = [1-(1-P1)2]P2 = [1(1-0,9)2]0,4 = 0,396. 4. При резервном соединении двух ненадежных элементов
Pc = P1[1-(1-P2)2] = 0,9[1-(1-0,4)2] = 0,576. Пример 2.2. В течение некоторого времени наблюдали за работой одного изделия. За весь период наблюдения зарегистрировано 10 отказов. До начала наблюдений изделие проработало 350 ч, к концу наблюдений наработка составила 2350 ч. Определить среднюю наработку на отказ и интенсивность отказов, полагая справедливым экспоненциальный закон плотности распределения вероятности отказов. Р е ш е н и е. Наработка изделия за период наблюдений t = t2 - t1 =2350-350=2000ч. Принимая
Интенсивность отказов lср = 1/tср = 1/200 = 0,005 1/ч Пример 2.3. Время работы изделия до отказа подчинено экспоненциальному закону распределения вероятностей отказов с параметром l = 2,5 10-5 1/ч. Определить характеристики P(t), Tсрпри t= 500; 1000; 2000 ч. Р е ш е н и е. Вероятность безотказной работы P(t) = exp [-lt] = exp [-2,5 10-5 t], P(500) = exp [-2,5 10-5 500]= 0,9875, P(1000) = exp [-2,5 10-5 1000]= 0,9753, P(2000) = exp [-2,5 10-5 2000]= 0,9512. Средняя наработка до первого отказа Tср = 1/l = 1/2,5 10-5 = 40000 ч При постоянной интенсивности отказов l равнонадежных основных и резервных элементов при ненагруженном резервировании вероятность безотказной работы
где n –число последовательно соединенных элементов основной системы; S – время (наработка); m – число резервных элементов. Пример 2.4. Определить вероятность безотказной работы машины, состоящей из четырех деталей, сгруппированных в три узла (рис.1).
Рис.1
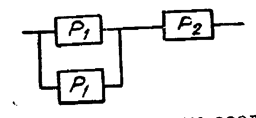
Вероятности безотказной работы деталей известны: P1=0,8; P2= 0,9, P3= 0,95; P4 = 0,98. Определим вероятность безотказной работы узлов: PI = P1 = 0,8 PII = P2 P3 = 09 095 = 0,855, PIII = P4 = 0,98 Вероятность безотказной работы машины Pм = PI PII PIII = 0,8 0,855 0,98 = 0,67 Для повышения надежности резервируется деталь в узле I(рис.2), тогда
Рис.2 PI` = 1 - (1 - P1)2= 1 - (1- 0,8)2 = 0,96 PII = P2 P3 = 0,855, PIII = P4 = 0,98 Pм = PI PII PIII = 0,96 0,855 0,98 = 0,81 т.е. безотказность возрастет более чем на 20 %. Если резервировать также детали в узле II, то получим Pм = 0,92, а при резервировании деталей в узле III получим Pм = 0,94. Данный расчет показывает, что наиболее эффективно резервирование наименее надежных деталей.
|

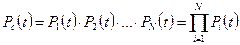 (19)
(19)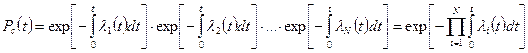
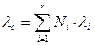 (21)
(21) ,
, 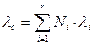 ,
, 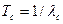 ,
, 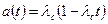 (22)
(22)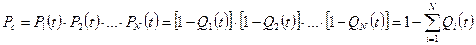 (23)
(23)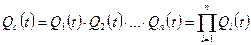 (24)
(24)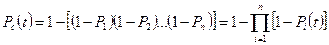 (25)
(25) (26)
(26)


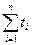 = 2000 ч, находим среднюю наработку на отказ
= 2000 ч, находим среднюю наработку на отказ