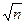РАСЧЕТ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ НЕВОССТАНАВЛИВАЕМЫХ ИЗДЕЛИЙ
Первый показатель - время безотказной работы (наработка до отказа). Для массы однотипных изделий это случайная величина. Закон ее распределения характеризуется так называемой п л о т н о с т ь ю р а с п р е д е л е н и я в е р о я т н о с т и о т к а з а f(t).
где п (t) - число отказавших изделий, т.е. вышедших из строя в интервале времени от t до (t +D t); N0 - первоначальное число испытываемых изделий; D t - интервал времени. Отношение называется ч а с т о т о й о т к а з о в. По величине частоты отказов можно судить о числе изделий, которые могут выйти из строя в каком-то промежутке времени, и соответственно установить необходимое количество запасных изделий. Пример 1.1. При наблюдении за эксплуатацией партии двигателей 500 шт. с ресурсом 300 ч зафиксировано число снятых двигателей в зависимости от времени наработки до отказа: время наработки t, ч 50 100 150 200 250 300 общее число отказавших двигателей N* t 20 24 30 34 40 50 Определим частоту отказов в интервале от 200 до 250часов. Количество отказавших изделий n(t) = N*250 – N*200 = 40 - 34 = 6; интервал времени Dt = 250 - 200 = 50 ч, первоначальное число двигателей N0 = 500; искомая частота отказов a(t)=n(t)/N0 Dt = 6/500 50 = 0,24 10-3 1/ч Если в аналогичных условиях эксплуатировать 250 двигателей, то можно определить, сколько двигателей может выйти из строя в промежутке от 200 до 250 ч работы: п (t) = a(t) N0 Dt = 0,24 10-3 250 50 =3 Следовательно, для нормальной работы необходимо иметь в резерве три двигателя. Определим общее число изделий, вышедших из строя к моменту времени t:
или, переходя к пределам,
Вероятность отказа
Таким образом, вероятность отказа есть интегральная функция распределения времени отказа. Вероятность безотказной работы
Отсюда следует, что
P (t) легко вычисляется по соотношению
или
где N*(t) - количество изделий, вышедших из строя к моменту времени t; N(t) - количество изделий, сохранивших работоспособность к моменту времени t Средняя наработка до отказа
ni (t) - количество изделий, вышедших из строя в интервале Dt, но ni (t)= ai(t) N0 Dt тогда
или в интегральной форме (D t ® 0, i®¥;). После преобразований получим
Пример 1.2. По данным Примера 1.1 определить вероятность безотказнойработы двигателя за ресурс. Время наработки (ресурс)составляет 300 ч, число отказавших двигателей N*t = 50, число испытанных двигателей N0 = 500. Вероятность безотказной работы P (t =300) = 1 – N*t/N0 = 1 - 50/500 = 0,9 Удобной характеристикой безотказности является также и н т е н с и в н о с т ь о т к а з о в - вероятность отказа в единицу времени, отнесенную к числу исправных изделий Nt на данный момент времени:
Величину l(t) легко выразить через рассмотренные ранее функции. С учетом (6) и (1) получим
Проинтегрировав выражение (5) с учетом (9) в пределах 0...t, получим
или
где N(t) – число образцов, исправно работающих к моменту t. Пример 1.3. Вычислить интенсивность отказов по данным Примера 1.1. Результаты вычислений приведены в таблице
где Nср (t) - число исправных двигателей, отнесенное к середине интервала Dt. Если постоянная интенсивность отказов l(t) = const, то согласно (10) вероятность безотказной работы
Согласно (5) плотность вероятностей отказа
Для l(t) = const среднее время безотказной работы tср есть величина, обратная интенсивности отказов:
Для высоконадежных систем, для которых lt < 0,1, можно воспользоваться приближенными формулами, разложив ехр [-lct]в ряд и ограничиться первыми двумя членами, тогда
Если средняя скорость износа постоянна, то распределение времени безотказной работы чаще всего подчиняется нормальному закону. В этом случае плотность распределения вероятности отказа
где tср- математическое ожидание случайной величины (наработка до отказа); s- среднее квадратичное отклонение, характеризующее рассеивание случайной величины около ее среднего значения. Если скорость износа непостоянна и постепенно уменьшается (упрочнение), то плотность распределения времени безотказной работы достаточно хорошо характеризуется логарифмически нормальным законом, т.е. логарифм времени безотказной работы распределен нормально:
Широко распространенное распределение Вейбулла хорошо характеризует устройства с большим числом одинаковых или близких по конструкции элементов (турбинные лопатки, подшипники качения и т.д.). В этом случае
где m, t0 - постоянные параметры, определяемые по результатам испытаний, const. При m =1 и t0 =1/l распределение Вейбулла превращается в экспоненциальное. Вероятность безотказной работы
Интенсивность отказов
Технологические и эксплуатационные дефекты наиболее часто характеризуются экспоненциальным, нормальным или распределением Вейбулла. Для того чтобы определить тип распределения по экспериментальным данным необходимо вычислить моменты распределения и параметры диаграммы:
где Ниже представлена диаграмма по которой возможно приблизительно определить тип распределения.
Оценка параметров для распределений, используемых при испытаниях на безотказность и в теории надежности: Экспоненциальное Нормальное Логарифмическое нормальное b2 = Вейбулла
В этих соотношениях s2=М2; Г(h) – гамма – функция (есть таблицы).
Параметр h связан с математическим ожиданием распределения Вейбулла Процедура проверки согласия опытного и теоретического распределения случайной величины x заключается в получении упорядоченного ряда результатов наблюдений этой величины
в построении на основании их функции накопленных частостей и сравнение этой функции с заданной теоретической. При использовании критерия l* определяют максимальное значение разности накопленной частости Fn(x) и вероятности F(x) Dn= max [Fn(x)- F(x)] И вычисляют ln*= Dn Задаются доверительной вероятностью g=Р(ln*£ln*табл) где ln*табл- табличное значение ln* для заданной доверительной вероятности g. Если ln*£ln*табл, то делают заключение, что нет оснований отвергать принятую гипотезу. Если ln*>ln*табл, то гипотезу отвергают.
|

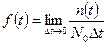 (1)
(1) (2)
(2)

 (3)
(3)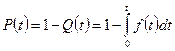 (4)
(4) (5)
(5)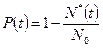 (6)
(6)
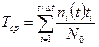

 (7)
(7)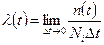 (8)
(8)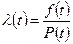 (9)
(9)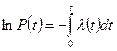
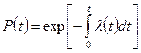 (10)
(10)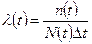
 (11)
(11)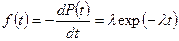 (12)
(12) =
= 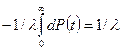


 (14)
(14)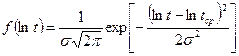 (15)
(15)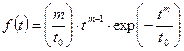 (16)
(16)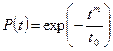 (17)
(17)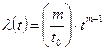 (18)
(18)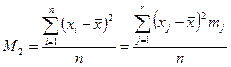 ;
; 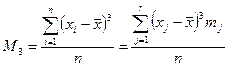 ;
; 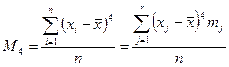 ;
;  ;
; 
 – эмпирическое среднее; mj – число значений в интервале j; n =åmj;
– эмпирическое среднее; mj – число значений в интервале j; n =åmj;  - число интервалов упорядоченного ряда наблюдений;
- число интервалов упорядоченного ряда наблюдений; 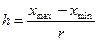 - длина интервала;
- длина интервала;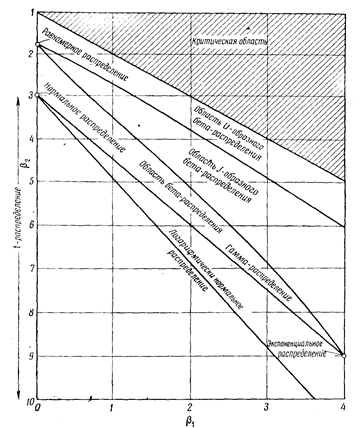
 =2,0; b2 =9,0.
=2,0; b2 =9,0.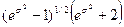 ;
;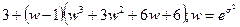
 ;
;
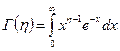 . Если h - положительное целое число, то Г(h)=(h-1)!
. Если h - положительное целое число, то Г(h)=(h-1)!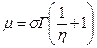 .
.