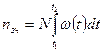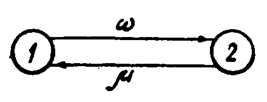РАСЧЕТ ХАРАКТЕРИСТИК БЕЗОТКАЗНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Основные показатели безотказности: Наработка на отказ Параметр потока отказов w(t) = n (Dt)/N Dt; n (Dt)- число изделий, отказавших в интервале от (t- 0,5 Dt) до (t + 0,5 Dt); N- число испытанных изделий; Dt- интервал времени. Коэффициент готовности Кг = tср /(tср + tв); tср - наработка на отказ; tв - среднее время восстановления. Коэффициент технического использования Кт.и = tср /(tср + tв + tт.о); tт.о -.время технического обслуживания. Показатели безотказной работы позволяют проводить различные расчеты, в том числе расчет потребности в запасных частях. Количество запасных частей nз.ч = w Dt N Для достаточно большой наработки (от t1до t2)
Пример 3.1. Интенсивность отказов изделия l= 0,02 1/ч; среднее время восстановления tв= 10 ч. Вычислить коэффициент готовности Кг . Р е ш е н и е. Средняя наработка до первого отказа Тср = 1/l = 1/0,002 = 50 ч Коэффициент готовности Кг= Тср /(Тср + tв) = 50/(50+10) = 0,83
Работоспособность системы описывается графом (рис. 5.4): состояние 1 - состояние работоспособности, состояние 2 - состояние отказа. Описание графа по приведенному правилу дает следующую систему уравнений вида (5.2): Z P1 (Z) - P1 (0) = -P1 (Z) w + P2 (Z) m, Z P2 (Z) - P2 (0) = P1 (Z) w - P2 (Z) m. Учитывая, что в момент включения t =0 система должна быть исправна: P1 (0) = l, Р2(0) = 0, получаем: Z P1 (Z) + P1 (Z) w - P2 (Z) m = 1, Z P2 (Z) + P2 (Z) m - P1 (Z) w = 0. Отсюда P2 (Z) = P1 (t) w/(Z+m), P1 (Z)= (Z+m)/[Z(Z+m +w)]. Обратное преобразование вероятности P1(Z) требует приведения ее к табличному виду. Для этого умножим и разделим P1(Z) на (w + m): P1(Z)={(Z+m)/[Z(Z+m+w)]}{(w+m)/(w+m)}= =[m (Z+m +w)+ Zw]/[Z(Z+w+w)(w+m)], P1(Z)=(1/Z)[m/ (w+m)]+[1/(Z+w+w)][ m/(w+m)]. Отсюда, учитывая, что 1/Z соответствует 1(t), а 1 /(Z +w+m) соответствует e-(m+w)t, получаем: P1(t)= [m/ (w+m)]+[w/(w+m)] e-(m+w)t. Анализом полученного выражения устанавливаем, что P1(t) при t Þ ¥ не может быть ниже величины m/(w+m). Эта постоянная часть, и является стационарным коэффициентом готовности изделия: m / (w+m)= (1/tв)/[(1/tв)+(1/tср)] = tср /(t ср + t в)= Kг. Постоянная времени экспоненты Тпэ = 1 /(w+m.). Переходный процесс длится 3¸4 Тпэ, после чего наступает установившийся режим. ПРИМЕР 5.3. Пусть w= 10-2 1/ч, a m = 1 1/ч. Тогда Тпэ = 1/(1+ 10-2)» 1 ч. Следовательно, переходный процесс длится 3¸4 часа, а далее надежность системы определяется стационарным коэффициентом готовности Kг = 1/(1+ 10-2) = 0,99.
|

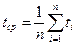 ; ti- время между соседними отказами; n- число отказов.
; ti- время между соседними отказами; n- число отказов.