ПРАКТИЧЕСКАЯ РАБОТА № 1. ИССЛЕДОВАНИЕ ЛИНЕЙЫХ СИСТЕМ
1. Цель работы: Исследование типовых линейных звеньев и их временных характеристик. 2. Задачи работы: Приобретение навыков в исследовании математической модели линейной системы, алгоритмической структуры звеньев, снятие временных характеристик. 3. КРАТКИЕ ТЕОРИТИЧЕСКИЕ СВЕДЕНИЯ: Общность математических выражений связывающих входные и выходные величины функционально различных элементов, позволяет выделить ограниченное число так называемых типовых алгоритмических звеньев. Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев. Классификацию типовых звеньев удобно осуществить, рассматривая различные частотные формы дифференциального уравнения a0 В таблице 1 приведены значения коэффициентов уравнений и названия для наиболее часто встречающихся звеньев. Переход от дифференциальной формы уравнения звена к операционной форме осуществляется заменой:
Передаточная функция W(p) = Таблица 1 Значения коэффициентов уравнения типовых звеньев
Основные характеристики типовых звеньев: - Амплитудно- и фазовочастотные характеристики АЧХ и ФЧХ; - Логарифмические характеристики ЛАЧХ и ЛФЧХ; - Амплитудно фазово частотная характеристика АФЧХ; - Корневой годограф (нули и полюса); - Переходной процесс; - Весовая функция. 4. ПРЕДВАРИТЕЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ: Ознакомиться с теоретическими сведениями по данной лабораторной работе, заранее составить передаточные функции по каждому из звеньев. 5. РАБОЧЕЕ ЗАДАНИЕ: 1. Используя выше перечисленный материал записать передаточные функции для каждого звена. 2. Создать передаточную функцию звена. 3. Используя пакет Mathlab построить основные характеристики для каждого из звеньев. (корневой годограф, переходной процесс, АЧХ и ФЧХ) 6. УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ: Выполняется эта работа записью звена в векторной форме:
|

 + a1
+ a1 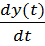 + a2y(t) = b0
+ a2y(t) = b0 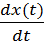 + b1x(t)
+ b1x(t) = p;
= p;  = p2…
= p2…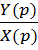
 2 Т2
2 Т2
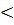 2 Т2
2 Т2



