ПРАКТИЧЕСКАЯ работа № 2. Устойчивость линейной системы автоматического управления. Влияние значения коэффициента усиления на устойчивость.
1. Цель работы: Анализ устойчивости системы автоматического управления. Определение насколько влияет изменение коэффициента усиления системы на устойчивость. 2. Задачи работы: Приобретение навыков при расчете устойчивости системы с использованием различных критериев и принципов. Определение влияния коэффициента усиления элемента на устойчивость работы всей системы автоматического регулирования. 3. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ: Устойчивость автоматической системы – это свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему из этого состояния. Математическое определение устойчивости: система является устойчивой, если свободная составляющая с течением времени стремится к нулю, т.е.
если же эта составляющая будет стремиться к вынужденной составляющей, то системы будет являться неустойчивой; и если свободная составляющая не стремиться ни к нулю, ни к бесконечности, то система находится на границе устойчивости. Условие устойчивости по корням характеристического уравнения: для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательными. Алгебраический критерий устойчивости: автоматическая система, описываемая характеристическим уравнением
устойчива если при Критерий Михайлова: автоматическая система управления, описываемая уравнением n–го порядка, устойчива, если при изменении ω от 0 до ∞ характеристический вектор системы F(jω) повернется против часовой стрелки на угол np/2, не обращаясь при этом в нуль. Критерий Найквиста: автоматическая система управления устойчива, если амплитудно-фазовая характеристика W(jω) разомкнутого контура не охватывает точку с координатами (-1; j0). Определение устойчивости системы по логарифмическим характеристикам: система является устойчивой, если амплитудно-логарифмическая характеристика этой системы раньше пересекает ось частоты, чем фазово-амплитудная характеристика ось -180°.
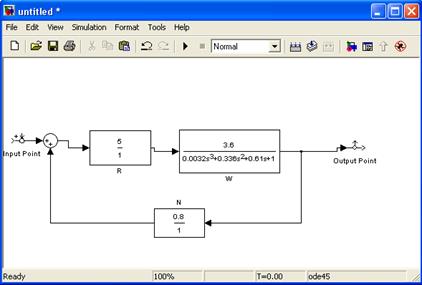
4. ПРЕДВАРИТЕЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ: Ознакомиться с теоретическими сведениями по данной работе, произвести расчеты по пунктам 1-2. Ознакомиться с указаниями по выполнению лабораторной работы. 5. РАБОЧЕЕ ЗАДАНИЕ: Определение устойчивости автоматической системы управления частотой вращения двигателя. Лабораторная работа проводится на базе комплексного пакета Mathlab, с использованием ПЭВМ. 1. Исходные данные. Принципиальная и алгоритмическая схемы автоматической системы управления частотой вращения двигателя приведены на рис.1
Рис. 1. Исходные данные к работе Исходные данные к системе автоматического управления: Передаточные функции всех элементов Передаточная функция двигателя по управляющему воздействию – е.д.с. генератора:
Передаточная функция генератора:
Тиристорный преобразователь практически может рассматриваться как безынерционное звено:
Операционный усилитель выполняет пропорциональное усиление:
Тахогенератор также является безынерционным звеном:
Таблица 1 Исходные данные по передаточным функциям
2. Упростить схему. Привести ее к виду
Рис. 2. Упрощенная схема САР. 3. Используя полученные данные после упрощения, произвести ввод данных: передаточные функции используя библиотеки, а затем и коэффициенты передаточных функций. 4. Зарисовать полученные графики: а. Годограф; б. Устойчивость по критерию Найквиста; в. Логарифмические характеристики. 5. По полученным данным сделать вывод об устойчивости данной системы. 2. Влияние значения коэффициента усиления на устойчивость системы. 1. Используется схема предыдущей части лабораторной работы. 2. Ввести вместо численного значения коэффициента усиления какого-нибудь элемента схемы различные значения. 3. Зарисовать графики при всех заданных значения коэффициента усиления: 4. Сделать выводы. 3. Влияние значения постоянной времени на устойчивость системы. 1. Используется схема предыдущей части лабораторной работы. 2. Ввести вместо численного значения постоянной времени какого-нибудь элемента схемы различные значения. 3. Зарисовать графики при всех заданных значения коэффициента усиления: 4. Сделать выводы. 6. УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ: Лабораторная работа проводится на базе комплексного пакета MATLAB с использованием ПЭВМ. В пакете MATLAB открывают библиотеку Simulink. Simulink – интерактивный инструмент пакета Mathlab для моделирования, имитации и анализа динамических систем. Он даёт возможность строить графические блок-диаграммы, имитировать динамические системы, исследовать работоспособность систем и совершенствовать проекты. Simulink полностью интегрирован с Mathlab, обеспечивая немедленный доступ к широкому спектру инструментов анализа и проектирования. Это можно сделать одним из трёх способов: □ Нажать кнопку □ В командной строке главного окна MatLab набрать Simulink и нажать клавишу □ Выполнить команду Open… в меню File и открыть файл модели (mdl-файл). 2. Создание нового документа. Для создания модели в среде Simulink необходимо последовательно выполнить ряд действий:
3. Из библиотеки Simulink выбирают необходимые блоки, компоненты и перетаскивают их в поле нового документа. Рисунку 2 соответствуют следующие блоки: Transfer Fcn, Sum, Input Point, Output Point. Для удобства поиск блоков рекомендуется производить путем ввода названия элемента в строке Find. Соединение блоков осуществляется указателем мыши при нажатой левой клавише (Рис.3.).
Рис.3. Алгоритмическая структура САР. Значения функций R, W, N задаются в меню Blok Parametres из контекстного меню (разделителем десятичных дробей является точка, ввод коэффициентов через пробел).
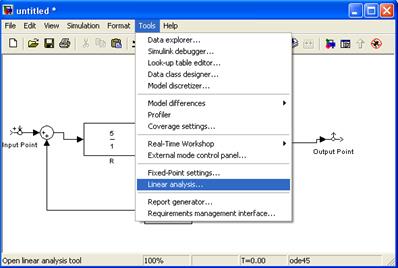
Рис.4. Параметры функции. 4. Для отображения графиков согласно заданию в меню Tool выбирают Linear analyses(рис.5).
Рис. 5. В появившемся окне LTI Viewer для настройки вида в меню Edit выбирают пункт Plot Configuration, в окне которого слева выбирают расположение и количество графиков на рабочем пространстве, справа – тип графика (рис.6). По получившимся графикам делают выводы об устойчивости САР.
Рис. 6.
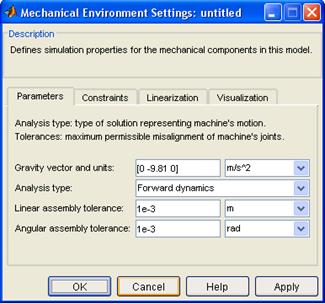
Рис.7. Вторую и третью части выполняют на той же модели, изменяя значения передаточного коэффициента системы в окне Blok Parametres (строка Numenator), и значений параметров в окне Mechanical environment (контекстное меню) по выбору.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Дать определение понятия устойчивости линейной САР. 2. Каковы должны быть корни характеристического уравнения устойчивой замкнутой САР? 3. Что такое предельный коэффициент усиления САР и методы его определения? 4. Как влияет изменение постоянных времени отдельных звеньев на устойчивость замкнутой САР? 5. Сформулируйте логарифмический критерий устойчивости. 6. Как определить понятие запасов устойчивости.
|



 ,
,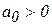 все диагональные определители матрицы больше нуля.
все диагональные определители матрицы больше нуля.
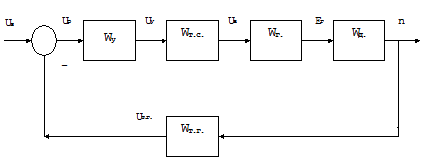
 ;
; ;
;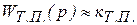 ;
;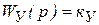 ;
;

 (Simulink) на панели инструментов командного окна MatLab.
(Simulink) на панели инструментов командного окна MatLab. Enter
Enter  на клавиатуре.
на клавиатуре. □ Создать новый файл модели с помощью команды File/New/ Model, или используя кнопку на панели инструментов.
□ Создать новый файл модели с помощью команды File/New/ Model, или используя кнопку на панели инструментов.