Настройка ПИ-регулятора скорости на симметричный оптимум.
Предположим, что выполнена настройка ПИ-регулятора тока, и передаточная функция оптимизированного контура тока выражается приближенной формулой (7). В этом случае передаточная функция разомкнутого контура скорости (см. рис. 4)
При стандартной настройке на симметричный оптимум параметры регулятора скорости выбирают так:
Подставив эти значения, получим
Регулятор компенсировал большую постоянную времени Тм и динамические свойства контура скорости опять определяются только малой постоянной времени
Для удобства анализа введем безразмерный оператор дифференцирования
Из (10) следует, что оптимизированный контур скорости представляет собой последовательное соединение инерционно-форсирующего звена и колебательного звена второго порядка. Амплитудно-частотная характеристика контура скорости, настроенного по симметричному оптимуму, представлена на рис. 3 (кривая 2). Наличие форсирующего члена в числителе приводит к появлению пика на частотной характеристикеристике. Характеристика построена для относительного значения частоты
В области низких частот функцию (10) можно упростить, приняв
Тогда приближенно
Или
Оптимизированный контур скорости можно приближенно представить колебательным звеном с эквивалентной постоянной времени Переходную функцию контура скорости найдем по (10), используя таблицы обратного преобразования Лапласа:
где
Наличие форсирующего звена в передаточной функции приводит к большому перерегулированию, достигающему 43%. Время первого достижения установившегося значения составляет 3,1 Перерегулирование уменьшается до 8%,- если на входе оптимизированного контура включить апериодический фильтр с постоянной времени способный компенсировать форсирующее звено в передаточной функции (9). В этом случае пик в частотной характеристике исчезает (кривая 3 на рис. 3). Асимптотическая логарифмическая частотная характеристика разомкнутого контура скорости, настроенного на симметричный оптимум состоит из трех отрезков прямых с наклоном - 40; -20 и -40 дБ/дек (система 2-1-2) и симметрична относительно частоты среза
Рис. 5. Асимптотическая ЛАХ контура скорости, настроенного на симметричный оптимум
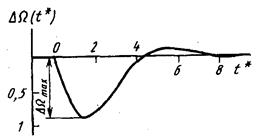
Рис.6. Переходная характеристика контура скорости по возмущению Рассмотрим динамические свойства оптимизированного контура скорости по возмущающему воздействию — моменту сопротивления. Под действиеммомента Мс скорость привода снижается на величину
Рассмотрим слагаемые входящие в эту передаточную функцию. Механическое сопротивление определяется механической инерционностью привода
Передаточная функция регулятора скорости, настроенного на симметричный оптимум, имеет вид
Учитывая, что
получим
Передаточная функция оптимизированного контура тока определяется по формуле (7). Подставив все передаточные функции в (12), получим
Наличие в числителе оператора дифференцирования р в качестве множителя показывает, что статическая ошибка контура скорости по возмущающему воздействию равна нулю. Найдем переходную функцию привода по возмущению, т. е. изменение скорости при внезапном скачкообразном приложении момента сопротивления (наброс нагрузки). Произведя преобразования (4.43), получим где На основе (14)получим переходную функцию при внезапном приложении нагрузки
Где
График этой функции при второго видно, что максимальное относительное снижение скорости (провал скорости) составляет 0,9. Откуда при МС=Мном
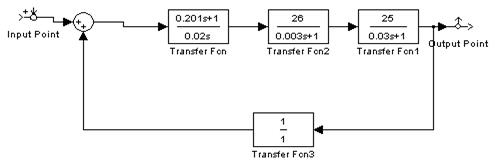
Провал скорости уменьшается при уменьшении малой некомпенсированной постоянной времени систему подчиненного регулирования можно анализировать численными методами на ЭВМ. Для этого используют уравнения переменных стояния и анализ проводят во временной области. Подобный анализ не накладывает никаких ограничений на настройку регуляторов. Параметры регуляторов выбирают по стандартной настройке или каким-либо другим способом. Нет также необходимости пренебрегать внутренней обратной связью по ЭДС. 4. ПРЕДВАРИТЕЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ Ознакомиться с теоретическими сведениями по данной работе, произвести расчеты по пунктам 1-2. Ознакомиться с указаниями по выполнению лабораторной работы. 5. Рабочее задание Настроить контуры регулирования САУ по принципу подчиненного регулирования. 1. Исходные данные. Алгоритмическая схема автоматической системы управления частотой вращения двигателя приведены на рис.7
Рис. 7. Исходные данные к системе автоматического управления: передаточная функция объекта управления по управляющему воздействию:
Передаточная функция преобразователя энергии:
Передаточная функция регулятора и типунастойке. Передаточная функция обратных связей
Исходные данные по передаточным функциям
2.Используя полученные данные соответствующего варианта произвести настройку системы, произвести ввод данных. 3.Зарисовать полученный график. 4.По полученным данным сделать вывод о длительности переходного процесса и величины перерегулирования каждого из контуров. 6. УКАЗАНИЕ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ Практическая работа проводится на базе комплексного пакета MATLAB с использованием ПЭВМ. 2. В пакете MATLAB открывают библиотеку Simulink. Это можно сделать одним из трёх способов: □ Нажать кнопку □ В командной строке главного окна MatLab набрать Simulink и нажать клавишу □ Выполнить команду Open… в меню File и открыть файл модели (mdl-файл). 2. Создание нового документа. Для создания модели в среде Simulink необходимо последовательно выполнить ряд действий:
3. Из библиотеки Simulink выбирают необходимые блоки, компоненты и перетаскивают их в поле нового документа. Рисунку 2 соответствуют следующие блоки: Transfer Fcn, Sum, Input Point, Output Point. Для удобства поиск блоков рекомендуется производить путем ввода названия элемента в строке Find.
Настройка ПИ-регулятора тока на технический оптимум(ОМ)
|

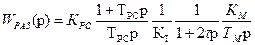
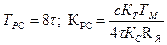 (8)
(8)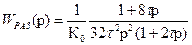
 . Передаточная функция замкнутого контура скорости
. Передаточная функция замкнутого контура скорости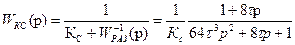 (9)
(9)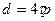 , тогда
, тогда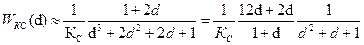 (10)
(10)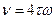
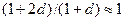
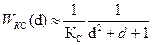
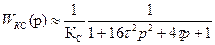
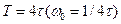 и коэффициентом демпфирования
и коэффициентом демпфирования 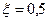 .
.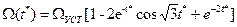 (11)
(11)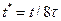 - безразмерное время.
- безразмерное время.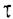 .
.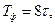
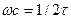 откуда метод и получил свое название (рис. 5).
откуда метод и получил свое название (рис. 5).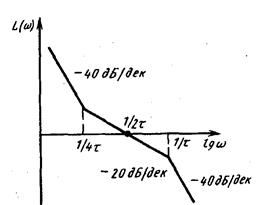
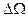 . Передаточную функцию по возмущению найдем на основании структурной схемы рис.2.
. Передаточную функцию по возмущению найдем на основании структурной схемы рис.2.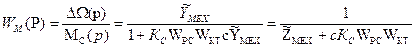 (12)
(12)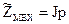
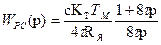
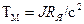
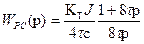
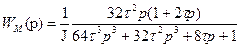 (13)
(13)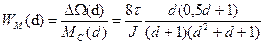 (14)
(14)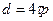
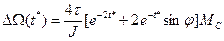
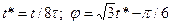
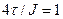 и
и 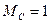 показан на рис.9
показан на рис.9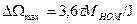 max
max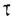 и уменьшении отношения номинального момента привода к моменту инерции
и уменьшении отношения номинального момента привода к моменту инерции 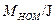 .. Сложную электромеханическую
.. Сложную электромеханическую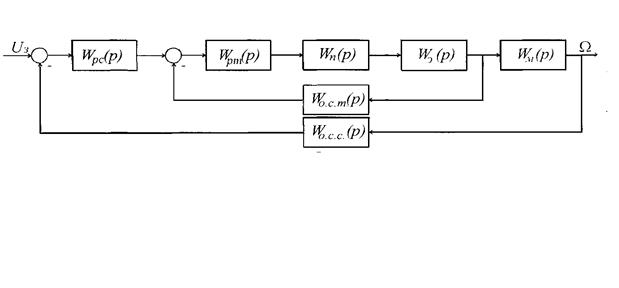
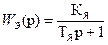
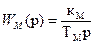
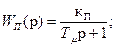
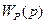
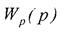 соответствует объекту
соответствует объекту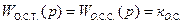
 (Simulink) на панели инструментов командного окна MatLab.
(Simulink) на панели инструментов командного окна MatLab. Enter
Enter  на клавиатуре.
на клавиатуре. □ Создать новый файл модели с помощью команды File/New/ Model, или используя кнопку на панели инструментов.
□ Создать новый файл модели с помощью команды File/New/ Model, или используя кнопку на панели инструментов.