Тема 3. Решение уравнения теплопроводности

Уравнение теплопроводности. Явная и неявная разностные схемы. Расчетные формулы.

 

Задание 3. Решение уравнения теплопроводности, одномерный случай, явная разностная схема.

Решить уравнение теплопроводности с помощью явной разностной схемы. Задание выполнить при h=0.1 для 0.0 ≤ t ≤ 100.0,

0.0 ≤ x ≤ 300.0. В контрольной работе сделать блок-схему программы и записать первые десять вычисленных значения температур.

Вариант № 1. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений

g₀ (x) = 2x(x+0.2)+0.4;

f₀ (t) = 2t+0.4;

f₁(t) = 1.36.

Вариант № 2. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = sin(x+0.45);

f₀ (t) = 0.435-2t;

f₁(t) = 0.8674.

Вариант № 3. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = 0.9+2x(1-x);

f₀ (t) = 3(0.3-2t);

f₁(t) = 1.38.

 

Вариант № 4. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = (x-0.2)(x+1)+0.2;

f₀ (t) = 6t;

f₁(t) = 0.84.

Вариант № 5. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений

g₀ (x) = sin(x+0.48);

f₀ (t) = 0.4618;

f₁(t) = 3t+0.882.

Вариант № 6 Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений

g₀ (x) = lg(2.63+x);

f₀ (t) = 3(0.14-t);

f₁(t) = 0.3075.

Вариант № 7. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = cos(x+0.845);

f₀ (t) = 6(t+0.11);

f₁(t) = 0.1205.

Вариант №8. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = lg(2.42+x);

f₀ (t) = 0.3838;

f₁(t) = 6(0.08-t).

Вариант № 9. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = 0.6+x(0.8-x);

f₀ (t) = 0.6;

f₁(t) = 3(0.24+t).

Вариант № 10. Найти приближенное решение уравнения ,

удовлетворяющее условиям

u(x, 0) = g₀ (x),u (0, t) = f₀ (t),u(L, t) = f₁ (t)

для значений 0 £ t £ T, 0 £ х £ L.

g₀ (x) = lg(1.43+2x);

f₀ (t) = 0.1553;

f₁(t) = 3(t+0.14).
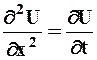