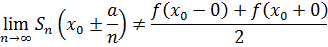Сходимость ряда Фурье. Явление Гиббса
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ Каждой абсолютно интегрируемой на отрезке* [—π, π] функции f(x) можно поставить в соответствие ее тригонометрический ряд Фурье:
Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера — Фурье:
Справедливо следующее утверждение. Если функция f(x) кусочно-гладкая на отрезке[—π, π], то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если
сумма тригонометрического ряда Фурье, то
для любого X ϵ [—π, π] и
Обозначим
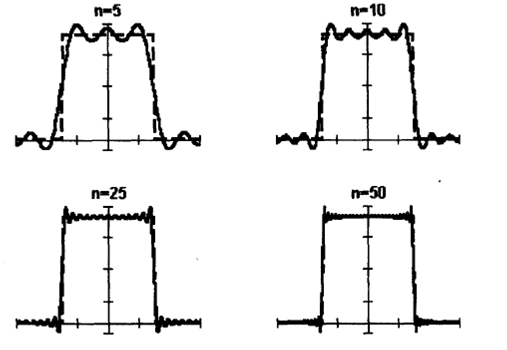
Ниже приведен фрагмент рабочего документа Mathcad с графиком функции*
и графики частичных сумм Sn(x) ее ряда Фурье.
На графиках видно, как сходятся частичные суммы ряда Фурье. В окрестности точек непрерывности функции f(x) разность между значением функции в точке х и значением частичной суммы ряда в этой точке стремится к нулю при n →
существуют такие последовательности un → x0 + 0 и vn → x0 - 0, что пределы Sn(un) и Sn(vn) при n Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Явление Гиббса состоит в том, что для некоторых функций f(x) в точке x0 ее скачка существуют такие значения α, что
Это утверждение не противоречит теории, поскольку у Гиббса рассмотрен предел Sn(xn), а в теореме — Sn(x).
|

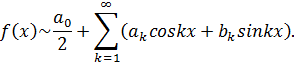
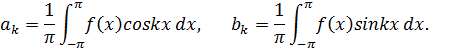
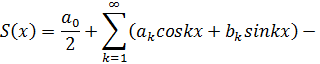


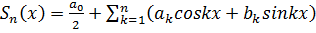 n-ю частичную сумму ряда Фурье кусочно-гладкой на отрезке [—π, π] функции f(x). Тогда утверждение теоремы можно записать в виде:
n-ю частичную сумму ряда Фурье кусочно-гладкой на отрезке [—π, π] функции f(x). Тогда утверждение теоремы можно записать в виде: , если f(x) непрерывна в точке х0;
, если f(x) непрерывна в точке х0; 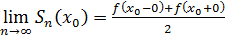 , если f(x) терпит разрыв первого рода (скачок) в точке х0.
, если f(x) терпит разрыв первого рода (скачок) в точке х0.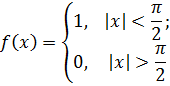
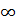 , что полностью соответствует теории, поскольку в этом случае
, что полностью соответствует теории, поскольку в этом случае  . Видно также, что разность Sn(x) — f(x) стремится к нулю тем скорее, чем дальше от точек разрыва функции расположена точка х. В окрестности точек разрыва x0 =
. Видно также, что разность Sn(x) — f(x) стремится к нулю тем скорее, чем дальше от точек разрыва функции расположена точка х. В окрестности точек разрыва x0 = 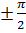 функции f(x) частичные суммы Фурье ведут себя иначе. При этом видно, что, хотя
функции f(x) частичные суммы Фурье ведут себя иначе. При этом видно, что, хотя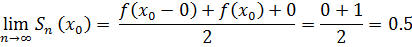
 различны и оба отличаются от
различны и оба отличаются от  .
.