Приближение функций. Минимальное свойство коэффициентов ФурьеФункция
где Uk, Vk — произвольные числа, называется тригонометрическим многочленом. Т ригонометрическим многочленом наилучшего приближения n-й степени функции f(x) на отрезке [—π, π] называется тригонометрический многочлен Рn(х)
Для любой ограниченной интегрируемой на [—π, π] функции f(x) частичная сумма Sn(x) ее ряда Фурье является тригонометрическим многочленом, наилучшего приближения n-й степени. ЗАДАНИЕ 3.34
Найдите для заданного значения погрешности е тригонометрический многочлен наилучшего приближения функции f(x) и наименьшей степени со среднеквадратичным отклонением, меньшим Ɛ. Постройте график зависимости среднеквадратичного отклонения от степени многочлена.
|
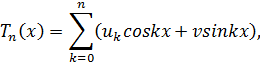
среднеквадратичное отклонение σn(х) которого от функции f(x) минимально:
