Исследуйте графически поведение частичных сумм ряда Фурье для функции

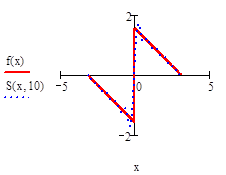
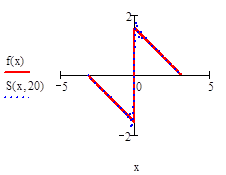
Постройте графики частичных сумм для n = 1, 2, 5,10, 20, 50. Вычислите значения частичных сумм ряда Фурье для n = 10, 20, 50 в точках X = —π, 0,  π.
π.
Примерный вариант выполнения задания приведен ниже.

Вычисление коэффициентов Фурье по формулам Эйлера — Фурье
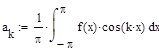

Вычисление частичной суммы ряда Фурье
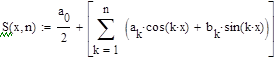

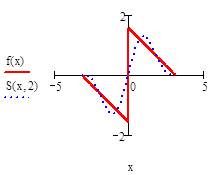 
|
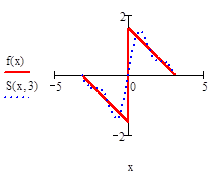
|

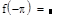
|
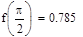
|
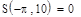
|
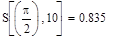
|

|
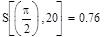
|
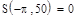
|

|

|
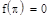
|
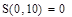
|

|

|
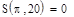
|

|

|
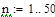
|

Указание. Для того чтобы определить функцию, заданную разными аналитическими выражениями на разных промежутках, лучше всего поступить следующим образом. Щелкнув в панели математических инструментов по кнопкам 
 откроите соответствующие панели и разместите их на рабочем документе, как показано на рис. 3.25. Введите имя функции переменной х, щелкните в панели калькулятора по кнопке присваивания
откроите соответствующие панели и разместите их на рабочем документе, как показано на рис. 3.25. Введите имя функции переменной х, щелкните в панели калькулятора по кнопке присваивания  , затем в панели программирования — по кнопке Add Llne. В рабочем документе справа от знака присваивания появится вертикальная черта с двумя помеченными строками для ввода. Перейдите в первую строку и щелкните по кнопке lf, введите слева от слова if выражение для вычисления функции, а справа — соответствующее ограничение на аргумент. При вводе выражений используйте кнопки панелей калькулятора, знаков отношений и греческого алфавита. Аналогично введите выражение во второй строке. Сохраните выражения для коэффициентов Фурье в виде векторов а и b. Для этого определите размерность вектора n равной 50 и определите диапазон изменения номера к компонент векторов а и b от 0 до п. Для того чтобы найти выражение для коэффициента Фурье аk, введите с клавиатуры а, знак нижнего индекса (нажмите клавишу <[>), введите в позиции нижнего индекса k, вернитесь в основную строку, введите знак присваивания и выражение для коэффициента. Аналогично определите выражения для коэффициентов bk. Частичную сумму ряда определите как функцию двух переменных - n и х. Прежде чем строить графики частичных сумм, задайте таблицу значений аргумента х на отрезке [—π, π] с некоторым шагом (в рассмотренном выше примере выбран шаг π/100). Численное исследование частичных сумм состоит в сравнении значений частичных сумм для различных N со значениями функции на концах отрезка, в точке скачка и в точке непрерывности. Введите имя функции (частичной суммы), указав в скобках нужное значение аргумента, и нажмите клавишу <=>, в результате на экране будет отображено значение функции в точке. Полезную информацию о поведении частичных сумм дает график зависимости значений от n
, затем в панели программирования — по кнопке Add Llne. В рабочем документе справа от знака присваивания появится вертикальная черта с двумя помеченными строками для ввода. Перейдите в первую строку и щелкните по кнопке lf, введите слева от слова if выражение для вычисления функции, а справа — соответствующее ограничение на аргумент. При вводе выражений используйте кнопки панелей калькулятора, знаков отношений и греческого алфавита. Аналогично введите выражение во второй строке. Сохраните выражения для коэффициентов Фурье в виде векторов а и b. Для этого определите размерность вектора n равной 50 и определите диапазон изменения номера к компонент векторов а и b от 0 до п. Для того чтобы найти выражение для коэффициента Фурье аk, введите с клавиатуры а, знак нижнего индекса (нажмите клавишу <[>), введите в позиции нижнего индекса k, вернитесь в основную строку, введите знак присваивания и выражение для коэффициента. Аналогично определите выражения для коэффициентов bk. Частичную сумму ряда определите как функцию двух переменных - n и х. Прежде чем строить графики частичных сумм, задайте таблицу значений аргумента х на отрезке [—π, π] с некоторым шагом (в рассмотренном выше примере выбран шаг π/100). Численное исследование частичных сумм состоит в сравнении значений частичных сумм для различных N со значениями функции на концах отрезка, в точке скачка и в точке непрерывности. Введите имя функции (частичной суммы), указав в скобках нужное значение аргумента, и нажмите клавишу <=>, в результате на экране будет отображено значение функции в точке. Полезную информацию о поведении частичных сумм дает график зависимости значений от n

Рис. 3.25. Панели инструментов для ввода функции с использованием панели программирования


 π.
π.
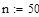

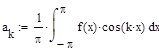

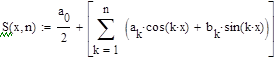







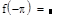
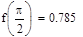
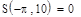
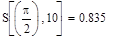

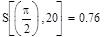
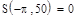


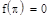
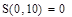


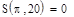


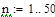


 откроите соответствующие панели и разместите их на рабочем документе, как показано на рис. 3.25. Введите имя функции переменной х, щелкните в панели калькулятора по кнопке присваивания
откроите соответствующие панели и разместите их на рабочем документе, как показано на рис. 3.25. Введите имя функции переменной х, щелкните в панели калькулятора по кнопке присваивания  , затем в панели программирования — по кнопке Add Llne. В рабочем документе справа от знака присваивания появится вертикальная черта с двумя помеченными строками для ввода. Перейдите в первую строку и щелкните по кнопке lf, введите слева от слова if выражение для вычисления функции, а справа — соответствующее ограничение на аргумент. При вводе выражений используйте кнопки панелей калькулятора, знаков отношений и греческого алфавита. Аналогично введите выражение во второй строке. Сохраните выражения для коэффициентов Фурье в виде векторов а и b. Для этого определите размерность вектора n равной 50 и определите диапазон изменения номера к компонент векторов а и b от 0 до п. Для того чтобы найти выражение для коэффициента Фурье аk, введите с клавиатуры а, знак нижнего индекса (нажмите клавишу <[>), введите в позиции нижнего индекса k, вернитесь в основную строку, введите знак присваивания и выражение для коэффициента. Аналогично определите выражения для коэффициентов bk. Частичную сумму ряда определите как функцию двух переменных - n и х. Прежде чем строить графики частичных сумм, задайте таблицу значений аргумента х на отрезке [—π, π] с некоторым шагом (в рассмотренном выше примере выбран шаг π/100). Численное исследование частичных сумм состоит в сравнении значений частичных сумм для различных N со значениями функции на концах отрезка, в точке скачка и в точке непрерывности. Введите имя функции (частичной суммы), указав в скобках нужное значение аргумента, и нажмите клавишу <=>, в результате на экране будет отображено значение функции в точке. Полезную информацию о поведении частичных сумм дает график зависимости значений от n
, затем в панели программирования — по кнопке Add Llne. В рабочем документе справа от знака присваивания появится вертикальная черта с двумя помеченными строками для ввода. Перейдите в первую строку и щелкните по кнопке lf, введите слева от слова if выражение для вычисления функции, а справа — соответствующее ограничение на аргумент. При вводе выражений используйте кнопки панелей калькулятора, знаков отношений и греческого алфавита. Аналогично введите выражение во второй строке. Сохраните выражения для коэффициентов Фурье в виде векторов а и b. Для этого определите размерность вектора n равной 50 и определите диапазон изменения номера к компонент векторов а и b от 0 до п. Для того чтобы найти выражение для коэффициента Фурье аk, введите с клавиатуры а, знак нижнего индекса (нажмите клавишу <[>), введите в позиции нижнего индекса k, вернитесь в основную строку, введите знак присваивания и выражение для коэффициента. Аналогично определите выражения для коэффициентов bk. Частичную сумму ряда определите как функцию двух переменных - n и х. Прежде чем строить графики частичных сумм, задайте таблицу значений аргумента х на отрезке [—π, π] с некоторым шагом (в рассмотренном выше примере выбран шаг π/100). Численное исследование частичных сумм состоит в сравнении значений частичных сумм для различных N со значениями функции на концах отрезка, в точке скачка и в точке непрерывности. Введите имя функции (частичной суммы), указав в скобках нужное значение аргумента, и нажмите клавишу <=>, в результате на экране будет отображено значение функции в точке. Полезную информацию о поведении частичных сумм дает график зависимости значений от n



