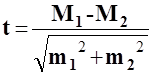Достоверность разности средних величин.
В медицинской практике часто приходится иметь дело не с одной, а с двумя средними: надо сравнивать среднюю длительность пребывания больных в 2-х стационарах или за отчетный год и предыдущий, исследуемую группу и контрольную и т.д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность, т.е. можно ли вывод о разности средних величин, полученный при выборочном исследовании, перенести на соответствующую генеральную совокупность. Достоверность разницы между двумя средними величинами измеряется доверительным коэффициентом (критерием Стьюдента t):
где М1 и М2- две средние арифметические величины, полученные в двух самостоятельных независимых группах наблюдений; m1 и m2 - их средние ошибки; t-доверительный коэффициент для разности средних. При t ³2 разность средних арифметических может быть признана существенной и не случайной, т.е. достоверной. Это значит, что и в генеральной совокупности средние величины отличаются, и при повторении подобных наблюдений будут получены аналогичные различия. Надежность такого вывода будет не меньше 95,5%. С увеличением t степень надежности также увеличивается, а риск ошибки (p) уменьшается. При t < 2 достоверность разности средних величин считается недоказанной.
|