Методом секущих
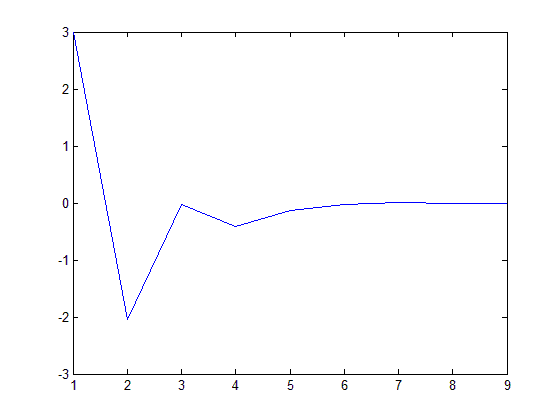
e=1e-08; %Устанавливаем допустимую погрешность x_k=3; %значение k-го приближения xk_minus_1=1; %значение k-1-го приближения I=0; %счётчик интераций I устанавливаем в ноль delta=x_k; D=[delta]; while abs(delta)>e%начало цикла интераций xk_plus_1=x_k-(fun(x_k)/(fun(x_k)-fun(xk_minus_1)))*(x_k-xk_minus_1); %следующее приближение delta=xk_plus_1 - x_k; %текущая погрешность D=[D delta]; xk_minus_1=x_k; x_k=xk_plus_1; %переприсваиваем приближения, чтоб перейти к следующему I=I+1; end; Str=['Значение корня: ' num2str(x_k)]; disp(Str) Str=['Точность: ' num2str(delta)]; disp(Str) Str=['Количество интераций: ' num2str(I)]; disp(Str) plot(D)
График приближения корня Значение корня: 0.35885 Точность: -1.0928e-009 Количество интераций: 8 2) Методом Ньютона e = 1e-08; %допустимая погрешность x_k = 1; %задаем значение первого приближения I = 0; %счетчик итераций I устанавливаем в ноль delta = x_k; D = [ delta ]; while abs(delta) > e %начало цикла итераций xk_plus_1 = x_k - fun(x_k) / fun1(x_k); %следующее приближение delta = xk_plus_1 - x_k; D = [ D delta ]; x_k = xk_plus_1; %переприсваиваем приближения, чтобы перейти к следующему I = I+1; end; Str = ['Значение корня: ' num2str(xk_plus_1) ]; disp(Str) Str = ['Точность: ' num2str(delta) ]; disp(Str) Str = ['Количество итераций: ' num2str(I) ]; disp(Str) plot(D)
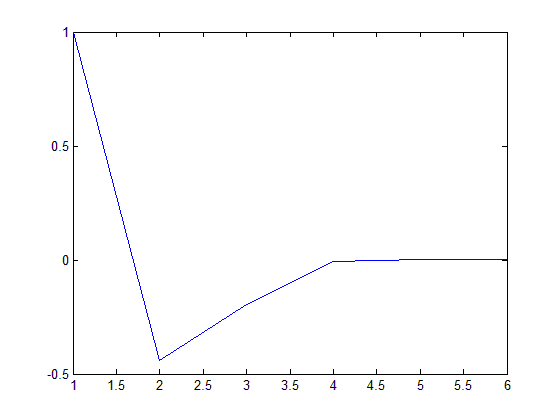
График приближения корня
Значение корня: 0.35885 Точность: 2.4741e-011 Количество итераций: 5
|