Метод Стеффенсена
В методе Ньютона необходимо на каждой итерации вычислять матрицу вторых производных. Поэтому, когда вычисление матрицы вторых производных требует больших объемов вычислений, трудоемкость каждой итерации значительно возрастает. Таким образом, требуется метод, который может обойти эту проблему. Одним из таких методов является метод Стеффенсена, который является разностным аналогом метода Ньютона. Матрица вторых производных заменяется разностным отношением первых производных градиента по специальным узловым точкам. Метод Ньютона. Пусть начальное приближение х0 известно. Заменим f(x) отрезком ряда Тейлора Вообще, если итерация хк известна, то следующее приближение xk+i в методе Ньютона определяется по правилу Метод Ньютона называют также методом касательных, так как новое приближение xk+i является абсциссой точки пересечения касательной, проведенной в точке (xh, f(xh)) к графику функции f(x), с осью Ох. Отметим без доказательства лишь две особенности этого метода. Во-первых, метод имеет квадратичную сходимость, т. е. в отличие от линейных задач погрешность на следующей итерации пропорциональна квадрату погрешности на предыдущей итерации. И, во-вторых, такая быстрая сходимость метода Ньютона гарантируется лишь при очень хороших, т. е. близких к точному решению, начальных приближениях. Если начальное приближение выбрано неудачно, то метод может сходиться медленно, либо не сойдется вообще.
|

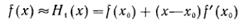 , и за следующее приближение x1 возьмем корень уравнения H1(x) = 0, т. е.
, и за следующее приближение x1 возьмем корень уравнения H1(x) = 0, т. е. 




