Теорема. Пусть в некоторой замкнутой окрестности 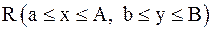 имеется одно и только одно решение
имеется одно и только одно решение  и
и 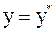 приведенной системы.
приведенной системы.
Тогда если:
1) функции 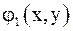 и
и 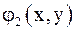 определены и непрерывно дифференцируемы в
определены и непрерывно дифференцируемы в  ;
;
2) начальные приближения  ,
, 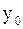 и все последующие приближения
и все последующие приближения  ,
,  принадлежат
принадлежат  ;
;
3) в  выполнены неравенства
выполнены неравенства 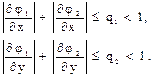 или
или
неравенства 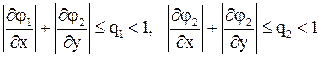 , то процесс последовательных приближений сходится к решению
, то процесс последовательных приближений сходится к решению  ,
, 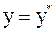 .
.
Оценка погрешности  -го приближения определяется неравенством:
-го приближения определяется неравенством:
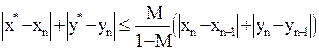 ,
,
где 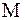 – наибольшее из чисел
– наибольшее из чисел  и
и  , входящих в эти неравенства.
, входящих в эти неравенства.
Сходимость метода считается хорошей, если  ; при этом
; при этом 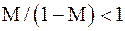 . Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.
. Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.
Метод секущих (метод хорд)
Если x0,x1 - приближенные значения корня уравнения f(x) = 0, а 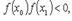 то последующие приближения находят по формуле
то последующие приближения находят по формуле
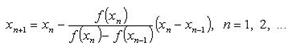 Методом хорд называют также метод, при котором один из концов отрезка
Методом хорд называют также метод, при котором один из концов отрезка 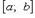 закреплен, т. е. вычисление приближения корня уравнения f(x) = 0 производят по
закреплен, т. е. вычисление приближения корня уравнения f(x) = 0 производят по
формулам: 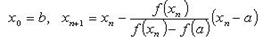 либо
либо 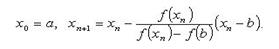
При этом предполагается, что корень уравнения находится на отрезке 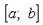 , а f ''(x) сохраняет знак на
, а f ''(x) сохраняет знак на  .
.

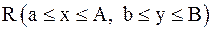 имеется одно и только одно решение
имеется одно и только одно решение  и
и 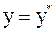 приведенной системы.
приведенной системы.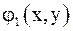 и
и 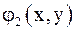 определены и непрерывно дифференцируемы в
определены и непрерывно дифференцируемы в  ;
; ,
, 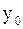 и все последующие приближения
и все последующие приближения  ,
,  принадлежат
принадлежат 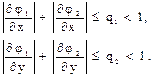 или
или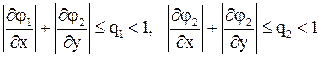 , то процесс последовательных приближений сходится к решению
, то процесс последовательных приближений сходится к решению  -го приближения определяется неравенством:
-го приближения определяется неравенством: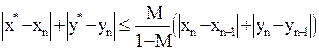 ,
,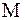 – наибольшее из чисел
– наибольшее из чисел  и
и  , входящих в эти неравенства.
, входящих в эти неравенства. ; при этом
; при этом 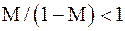 . Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.
. Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.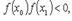 то последующие приближения находят по формуле
то последующие приближения находят по формуле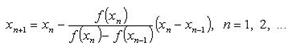 Методом хорд называют также метод, при котором один из концов отрезка
Методом хорд называют также метод, при котором один из концов отрезка 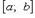 закреплен, т. е. вычисление приближения корня уравнения f(x) = 0 производят по
закреплен, т. е. вычисление приближения корня уравнения f(x) = 0 производят по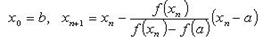 либо
либо 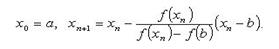
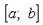 , а f ''(x) сохраняет знак на
, а f ''(x) сохраняет знак на  .
.


