Цикл Карно и его КПД для идеального газа
Круговой процесс, состоящий из двух изотерм и двух адиабат, называют циклом Карно. Как показал Карно, этот процесс независимо от природы рабочего тела обладает наибольшим КПД. Пусть рабочим телом будет идеальный газ в количестве 1 кмоль. Цикл состоит из 4-х процессов (рис. 62).
1. Рабочее тело с параметрами (P1,V1,T) – точка 1, приводится в контакт с нагревателем постоянной температуры T = const и бесконечно большой внутренней энергией. Газ изотермически расширяется от состояния 1 до состояния 2. При изотермическом расширении на участке 1-2 от нагревателя отбирается теплота Q, численно равная работе при изотермическом процессе
2. В точке 2 с параметрами (P2,V2,T) нагреватель отсоединяется от рабочего тела и при тепловой изоляции, т.е. адиабатически, расширяется из состояния 2 в состояние 3. В результате этого процесса рабочее тело охлаждается до температуры Т0, внутренняя энергия его уменьшается, и оно переходит в состояние 3 с параметрами (P3, V3, T0). 3. В точке 3 рабочее тело приводят в контакт с холодильником при температуре Т0 < T и газ изотермически сжимают до состояния 4. При этом от рабочего тела отбирается теплота Q0, эквивалентная работе при изотермическом сжатии газа
и тело переходит в состояние с параметрами (P4,V4,T0). 4. Рабочее тело отсоединяют от холодильника и газ адиабатически сжимают до исходного состояния 1 с параметрами (P1,V1,T). При этом внутренняя энергия возрастает и температура повысится до первоначального значения Т. КПД цикла будет равен отношению полезной работы А газа, совершенной за один цикл A = Q – Q0, к затраченной энергии, т.е. подведенной от нагревателя теплоте Q
Здесь Q, Q0, T, T0 - соответственно теплота, отобранная от нагревателя и переданная холодильнику, температура нагревателя и температура холодильника. Точки 2 и 3 лежат на адиабате и для них можно записать
Разделив почленно эти равенства, получим V2/V1 = V3/V4 и тогда выражение для КПД цикла Карно будет иметь вид
где Т и Т0 - температуры нагревателя и холодильника. Видно, что η = 1 только при Т0 = 0, и поскольку такая температура недостижима, то η всегда < 1. Реальные машины, работе которых сопутсвуют необратимые потери энергии, имеют КПД η' еще меньше, чем η
Существует также обратный цикл Карно, в котором за счет работы энергия отбирается от холодного тела и передается нагретому. По этой схеме работают холодильные машины. Обратный цикл имеет следующие стадии: 1. Адиабатное расширение 1– 4 с понижением температуры от Т до Т0. 2. Изотермическое расширение 4—3 с отбором теплоты 3. Адиабатное сжатие 3-2 с возрастанием температуры от Т0 до Т. 4. Изотермическое сжатие 2-1, сопровождаемое отводом теплоты В обратном цикле
|



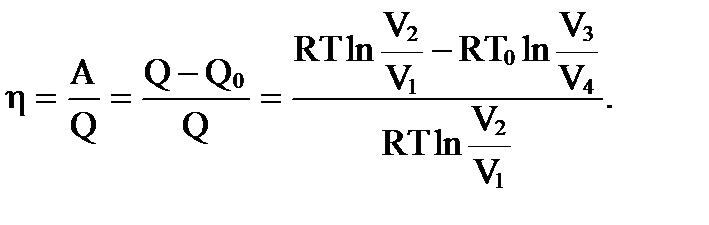
 Аналогичную запись можно сделать для точек 1 и 4:
Аналогичную запись можно сделать для точек 1 и 4:
 ,
,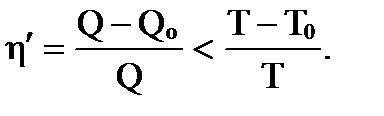
 от холодильника.
от холодильника. .
. и работа, совершаемая за один цикл газом отрицательна (А < 0) т.е. над газом совершается работа А внешними силами (А' = -А). За счет этой работы энергия в форме теплоты переносится от холодного тела к горячему. Подобные циклы имеют место в холодильных машинах. КПД обратного цикла Карно имеет вид
и работа, совершаемая за один цикл газом отрицательна (А < 0) т.е. над газом совершается работа А внешними силами (А' = -А). За счет этой работы энергия в форме теплоты переносится от холодного тела к горячему. Подобные циклы имеют место в холодильных машинах. КПД обратного цикла Карно имеет вид



