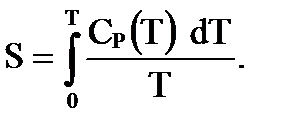Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от тела менее нагретого к телу более нагретому.
Из второго закона термодинамики вытекает вывод о невозможности построения вечного двигателя второго рода, действующего за счет охлаждения одного источника теплоты(например, путем отбора внутренней энергии у мирового океана или из больших водоемов). Теорема Нернста позволяет определить значение энтропии в каждом состоянии. Поскольку в пределе при Т→ 0 значение энтропии равно 0
Энтропия и вероятность Энтропия изолированной и предоставленной самой себе системы не может убывать. С другой стороны, очевидно, что предоставленная сомой себе система будет переходить из менее вероятных состояний в более вероятные. Таким образом энтропия и вероятность изолированной системы ведут себя сходным образом: они могут либо возрастать, либо оставаться неизменными. Между энтропией S и термодинамической вероятностью w системы существует определенная связь, которая, как показал Больцман, имеет следующий вид S = k ln w, где k – постоянная Больцмана. Известно, что математическая вероятность некоторого события равна отношению числа случаев, благоприятствующих данному событию, к общему числу равновозможных случаев и она не может быть больше единицы. Под термодинамической вероятностью понимают число различных способов, которыми может быть осуществлено данное состояние. Чтобы понять смысл величины w рассмотрим следующий пример. Пусть в сосуде имеется только две молекулы. Мысленно разделим сосуд на две равные части – левую и правую и подсчитаем число состояний, отличающихся друг от друга числом молекул в левой и правой частях сосуда. Для этого пронумеруем молекулы х1 и х2
Рис. 63 и подсчитаем число способов, которыми может быть реализовано каждое состояние. Вследствие движения молекул их распределение между обеими частями будет изменяться, как показано на рис. 63. Для двух молекул число таких способов оказалось равным 4. Из 4-х возможных распределений молекул между половинами сосуда 2 соответствуют одинаковому количеству молекул справа и слева и двумя способами получены состояния, при которых обе молекулы оказываются в одной из половин сосуда. Полное число способов распределения для произвольного числа N частиц равно w= 2N. В приведенном примере их оказалось 4.
|

 , то значение энтропии системы при температуре
, то значение энтропии системы при температуре  , если известна ее теплоемкость, определяется интегралом
, если известна ее теплоемкость, определяется интегралом