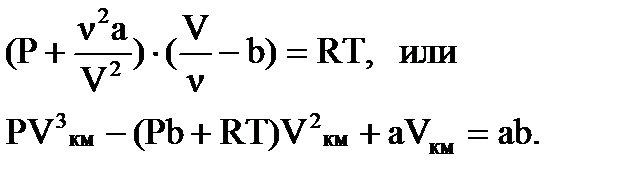Для определения состояния реальных газов из большого числа предложенных уравнений самым простым оказалось уравнение Ван-дер
Ваальса. Это уравнение получено введением соответствующих поправок в уравнение состояния PVкм = RT для одного кмоля
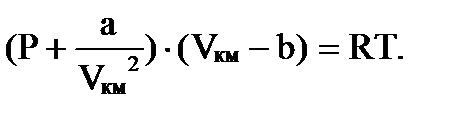
Здесь Р – давление газа на стенки сосуда, a и b - константы Ван-дер-Ваальса, значения которых определяют опытным путем и которые имеют различные значения для разных газов.
Константа b учитывает ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров. Эта константа равна учетверенному объему самих молекул.
Поправка 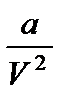 учитывает внутреннее давление Pi, обусловленное взаимным притяжением молекул друг к другу, т.е. это как бы добавочное давление. Если учесть, что V = νVкм, то для произвольного числа киломолей с учетом
учитывает внутреннее давление Pi, обусловленное взаимным притяжением молекул друг к другу, т.е. это как бы добавочное давление. Если учесть, что V = νVкм, то для произвольного числа киломолей с учетом 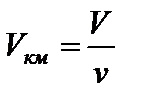 получим
получим
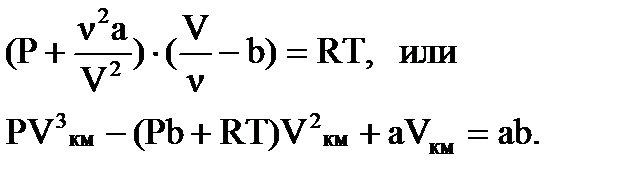
Как видно, это кубическое уравнение относительно объема V, коэффициенты которого зависят от давления Р и температуры Т. Кубическое уравнение со свободным членом и вещественными коэффициентами имеет
три решения. Причем в зависимости от соотношения между коэффициентами либо
все три
решения вещественные, либо одно - вещественное, а два – комплексные. Поскольку объем может быть только вещественным, то комплексные решения не имеют физического смысла. График теоретических изотерм Ван-дер-Ваальса для нескольких значений Т (Т4 > Тк > Т3 >Т2 > T1) представлен на рис. 66. Начиная с определенной своей для каждого вещества температуры Ткр при любом давлении вещественным оказывается только одно решение уравнения. Температура Ткр называется критической. Если повышать температуру, то точки, соответствующие решениям уравнения V1, V2, V3 все больше сближаясь, сливаются в одну точку, обозначенную буквой К.
Точка К называется критической.
Для получения экспериментальных изотерм берут сосуд с перемещающимся поршнем и начинают сжимать газ, измеряют объем и давление и следят, чтобы температура оставалась постоянной. Вначале с уменьшением объема давление газа растет, причем ход изотермы (на участке 1-2 рис. 67) довольно хорошо описывается уравнением Ван-дер-Ваальса. Однако, начиная с некоторого значения объема Vг, давление в сосуде перестает меняться, само вещество перестает быть однородным, часть газа конденсируется в жидкость. Происходит, как говорят, расслоение вещества на две фазы: жидкую и газообразную. По мере дальнейшего уменьшения объема (на участке 2-3) все большая часть вещества переходит в жидкую фазу при постоянном давлении. После того как процесс конденсации заканчивается (в точке 3) дальнейшее уменьшение объема сопровождается резким увеличением давления (жидкости практически несжимаемы), причем кривая вновь хорошо следует уравнению Ван-дер-Ваальса.
Таким образом, уравнение Ван-дер-Ваальса описывает не только газообразное состояние вещества, но также процесс перехода в жидкое состояние и процесс сжатия жидкости. Отличие экспериментальных изотерм от теоретических наблюдается на участке 2-3 (вместо S-образного витка имеем прямую). В состояниях, соответствующих горизонтальному участку изотермы, наблюдается равновесие между жидкой и газообразной фазами. Газ (или пар), находящийся в равновесии со своей жидкостью, называется насыщенным паром, а соответствующее давление называют давлением насыщенного пара.
На рис. 68 приведены экспериментальные изотермы для нескольких
значений Т. Как видно, с повышением температуры Т горизонтальный участок изотермы сокращается, стягиваясь в точку – при Т = Ткр. Давление насыщенного пара растет с температурой, достигая в критической точке значения Ркр. Состояние вещества, имеющего критические параметры Vкр, Ркр, Ткр называют критическим. В системе обладающей параметрами выше критических, исчезает различие между жидкостью и паром. Плотность жидкости и насыщенного пара становится одинаковой. При температуре выше Ткр вещество при любом давлении оказывается однородным. При таких температурах никаким сжатием невозможно превратить пар (или газ) в жидкость.
Если через крайние точки горизонтальных участков изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний (рис. 69). Колоколообразная кривая и участок критической изотермы I-К делят диаграмму (PV) на 3 области:
- область однородных жидких состояний (ж),
- область двухфазных состояний (ж-п) – жидкость + пар,
- область однородных газовых состояний (г,п).
В последней можно выделить две подобласти:
П – под правой ветвью изотермы – область пара: вещество, находящееся в состоянии, соответствующем этой области диаграммы, может быть изотермически превращено в жидкость;
Г – над критической изотермой: вещество, находящееся в одном из состояний при температуре выше критической, не может быть сжижено никаким сжатием.

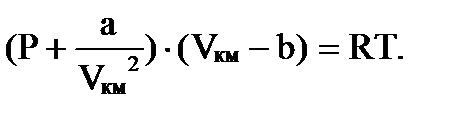
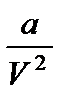 учитывает внутреннее давление Pi, обусловленное взаимным притяжением молекул друг к другу, т.е. это как бы добавочное давление. Если учесть, что V = νVкм, то для произвольного числа киломолей с учетом
учитывает внутреннее давление Pi, обусловленное взаимным притяжением молекул друг к другу, т.е. это как бы добавочное давление. Если учесть, что V = νVкм, то для произвольного числа киломолей с учетом 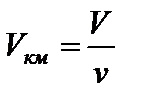 получим
получим