Термическое уравнение состояния
Выше говорилось, что в термодинамическом равновесии внутренние параметры являются функциями внешних параметров и температуры. В частности, опыт показывает, что для сжимаемых сред (газов, жидкостей) в равновесном состоянии давление, объем и температура находятся в функциональной зависимости
f (p, V, T) = 0. (8.1)
Это термическое уравнение состояния сжимаемых сред в общем виде. Какой параметр (давление или объем) считать внешним, а какой внутренним, зависит от конкретной задачи. Вид функциональной зависимости различен для разных сред. Для идеального газа термическим уравнением состояния является уравнение Клапейрона–Менделеева
pV = ν RT, или p = ν RT / V. (8.2)
Здесь ν – число молей газа, R = 8,314 Дж / (моль × К) – универсальная газовая постоянная (одна и та же для всех газов). Для смеси идеальных газов имеет место закон Дальтона: давление смеси p равно сумме парциальных давлений pi компонент
p =
Так как число молей смеси ν = Sν i, то уравнение состояния смеси идеальных газов имеет тот же вид, что и для химически однородного идеального газа. Реальные газы лишь приблизительно следуют уравнению Клапейрона–Менделеева. Существует ряд моделей, учитывающих реальные свойства газов. Наиболее известной является модель газа Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса имеет вид
p = ν RT / (V – ν b) – a ν2 / V 2, (8.3)
где a и b – постоянные, различные для конкретных газов. В этом уравнении учитывается конечный размер молекул и их взаимодействие. Модель описывает жидкие и газообразные состояния вещества, а также переход жидкости в газ и наоборот. Термическое уравнение состояния принадлежит к числу важнейших характеристик макроскопических свойств физически однородных тел. Его нельзя получить из общих принципов термодинамики. Термодинамика заимствует его из опыта либо статистической физики. Макроскопическая система необязательно может характеризоваться давлением и объемом, но также другими параметрами. Например, гальванический элемент характеризуется эдс E и проходящим зарядом e (уравнение состояния в этом случае может быть вида E = E (T)); мыльная или иная пленка – поверхностным натяжением σ и площадью S (уравнение состояния будет σ = σ(T)), диэлектрик – поляризацией P и напряженностью электрического поля E (для изотропного диэлектрика эти величины связаны уравнением P = (ε(T) – 1) / 4π × E, ε(T) – диэлектрическая проницаемость, зависящая от температуры) и т. д. Термическое уравнение состояния связывает обобщенные силы с внешними параметрами, являющимися обобщенными координатами, и с температурой. Система может характеризоваться не одним термическим уравнением состояния. Этот вопрос будет затронут при рассмотрении работы, совершаемой системой.
|

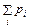 .
.


