Внутренняя энергия. Внутренняя энергия термодинамической системы определяется как полная энергия, заключенная в системе (за вычетом кинетической и потенциальной энергии ее центра
Внутренняя энергия термодинамической системы определяется как полная энергия, заключенная в системе (за вычетом кинетической и потенциальной энергии ее центра масс). С точки зрения молекулярных представлений, внутренняя энергия системы равна сумме кинетической энергии теплового движения молекул и энергии их взаимодействия. Первое начало термодинамики утверждает, что внутренняя энергия является функцией состояния. Отсюда следует, что для циклического процесса U 2 = U 1 и A ' + Q + Z = 0. Система производит работу A = – A ' над окружающей средой, получая от нее энергию Q + Z: A = Q + Z (для закрытой системы A = Q). Вечный двигатель первого рода должен был бы только совершать работу над окружающей средой, ничего не получая от нее. Следовательно, первое начало термодинамики можно назвать также принципом невозможности вечного двигателя первого рода. Для равновесного кругового процесса можно написать
Это означает, что дифференциал dU внутренней энергии полный. Внутренняя энергия определяется в термодинамике не однозначно, а с точностью до произвольной аддитивной постоянной. Выбрав некоторое состояние за нулевую точку отсчета внутренней энергии, можно фиксировать эту постоянную. Реальное значение в термодинамике имеет разность значений внутренней энергии в различных состояниях. Поэтому указанная постоянная не существенна. Как внутренний равновесный параметр внутренняя энергия U является функцией температуры T и внешних параметров xi (i = 1,..., n): U = U (T, x 1,..., xn). (11.1)
Это калорическое уравнение состояния. Оно устанавливается опытным путем. Его можно получить методами статистической физики. Если известны термические уравнения состояния, то, пользуясь аппаратом термодинамики, можно найти зависимость внутренней энергии от внешних параметров. Газы – простые системы (системы с двумя степенями свободы). Их состояние описывается температурой и одним внешним параметром (пусть это будет объем V). Поэтому для газов калорическое уравнение состояния имеет вид
U = U (T, V). (11.2)
В результате опытов Гей-Люссака и Джоуля установлен закон Джоуля о независимости внутренней энергии идеального газа от объема.
Работа
Элементарная работа над газом, входящая в уравнение (10.3), вычисляется по формуле
δ A ' = – pedV,
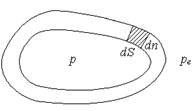
где pe – внешнее давление (предполагается, что других внешних сил, кроме сил давления, нет). Это выражение для δ A ' легко получить, если рассмотреть газ в цилиндре под поршнем, на который снаружи действует давление pe (рис. 2). При перемещении поршня на dx внешнее давление совершает работу δ A ' = – Fedx = – peSdx = – pedV. Несложно получить выражение для δ A ' и в случае, когда газ находится в эластичной оболочке, а внешнее давление также равно pe (рис. 3). Пусть на участке dS оболочка перемещается по внешней нормали на dn. Тогда δ A ' = – pedS × dn. Произведение dS × dn дает элементарный объем, а интегрирование по S приводит к искомому выражению. Если процесс расширения (сжатия) равновесный, то давление газа равно наружному: p = pe и работа системы (газа) равна
δ A = pdV. (12.1)
При изменении объема от V 1 до V 2 работа сжимаемой среды (не только газа) в равновесном процессе выражается интегралом (речь идет о работе сил давления)
A 12 =
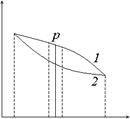
Элементарная работа в общем случае (и в частности, выражение (12.1) для газа) не является полным дифференциалом какой-либо функции состояния (поэтому для дифференциально малой работы используется специальное обозначение, отличающее ее от полных дифференциалов). Соответственно этому криволинейный интеграл (12.2) зависит от пути перехода системы из начального состояния в конечное. Это становится особенно ясным, если рассмотреть графическую интерпретацию работы на (p, V)-диаграмме (рис. 4).
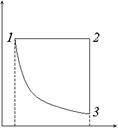
Произведение pdV дает площадь элементарного прямоугольника. Интегрирование затем по V (суммирование элементарных прямоугольников) дает всю площадь под кривой: работа численно равна площади под кривой перехода. Кривые 1 и 2 соответствуют двум разным процессам при одном и том же начальном и совпадающих конечных состояниях. Для процесса 1 площадь больше. Итак, работа системы не определяется только начальным и конечным состояниями, а зависит еще от процесса перехода. Другими словами, не существует величины A, приращением или убылью которой была бы δ A. Работа имеет смысл лишь при указании условий сжатия или расширения газа. Если задана кривая p = p (V), то интеграл в выражении (12.2) можно вычислить. Просто это сделать для идеального газа. Его термическое уравнение состояния имеет вид (8.2). В изотермическом процессе T = const и работа
A 13 =
– площадь под гиперболой 1–3 на рис. 5. В изобарическом процессе p = const и работа
A 12 =
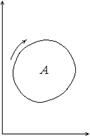
– площадь под отрезком 1–2 прямой, параллельной оси V. Из точки 2 на диаграмме можно перейти в точку 3 по изохоре 2–3 (V = const), при этом работа не будет совершаться. Переходы из точки 1 в точку 3 по изотерме и по изобаре-изохоре сопровождаются разной величиной произведенной работы. При круговом процессе работа A численно равна площади цикла (рис. 6). Если точка, изображающая состояние системы, перемещается по часовой стрелке, то работа системы положительна, а если цикл проходится в направлении против часовой стрелки, то отрицательна. Следует еще раз подчеркнуть, что равновесное состояние газа вполне определяется заданием двух параметров, например T и V или p и V (третий параметр находится из уравнения (8.1)). Газ – простая система. На диаграмме равновесное состояние газа изображается точкой, а равновесный процесс – кривой. Неравновесные состояния системы, в том числе газа, если и можно описать, то только с помощью очень большого числа параметров. Неравновесные состояния газа нельзя изобразить точкой, к примеру, на (p, V) - диаграмме; не изображаются на ней и неравновесные процессы. Состояния системы с многими степенями свободы определяются температурой T и внешними параметрами xi (i =1,..., n). В этом случае работа по-прежнему зависит от пути перехода, а вместо формулы (12.1) следует писать
δ A = X 1 dx 1 + X 2 dx 2 +... + Xndxn =
Величины xi носят название обобщенных координат, а Xi – обобщенных сил (Xi являются функциями температуры и обобщенных координат; эти зависимости называются термическими уравнениями состояния). Так, элементарная работа однородной деформации единицы объема твердого тела равна
δ A = –
где ε ij – компоненты деформации (растяжения и сдвига), σ ij – нормальные и сдвиговые компоненты напряжения. Другие примеры выражений для элементарной работы системы: работа сил поверхностного натяжения при изменении площади поверхности на d S равна δ A = – σ d S (σ – поверхностное натяжение); работа эдс E гальванического элемента при прохождении заряда de есть δ A = Ede; элементарная работа диэлектрика в электрическом поле напряженности
δ A = – V / 4π × (
где
δ A = – V / 4π × EdD,
где E и D – величины напряженности электрического поля и электрической индукции соответственно.
|

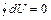 .
.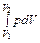 . (12.2)
. (12.2)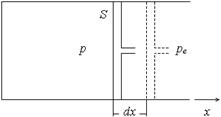
 = ν RT · ln(V 2 / V 1)
= ν RT · ln(V 2 / V 1)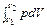 = p (V 2 – V 1)
= p (V 2 – V 1)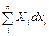 . (12.3)
. (12.3)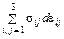 ,
,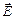 равна
равна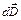 ) = – V / 4π × (ExdDx + EydDy + EzdDz),
) = – V / 4π × (ExdDx + EydDy + EzdDz),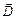 – вектор электрической индукции. Для изотропного диэлектрика имеет место соотношение
– вектор электрической индукции. Для изотропного диэлектрика имеет место соотношение 


