В идеальном газе
Для одного моля идеального газа первое начало термодинамики с учетом (15.6) принимает вид
δ Q = cV dT + pdV.
Если процесс адиабатический, то δ Q = 0 и
cV dT + pdV = 0.
Из термического уравнения состояния следует: T = pV / R и dT = (pdV + Vdp) / R. Величина dT исключается, для cV используется ее выражение через универсальную газовую постоянную R и показатель адиабаты γ, и после несложных преобразований получается дифференциальное уравнение
γ pdV + Vdp = 0.
Оно решается методом разделения переменных:
dp / p + γ dV / V = 0 ® ln p + γ · ln V = const ® pV γ = const 17.1)
– уравнение адиабатического процесса в идеальном газе (уравнение Пуассона). Отсюда ясен смысл названия для γ. Кривые (17.1) на (p, V) - диаграмме называются адиабатами Пуассона (в термодинамике просто адиабатами). Для газов γ > 1. Поэтому на (p, V )-диаграмме адиабаты падают круче изотерм. Это остается справедливым и с учетом реальных свойств газов (в области устойчивых состояний). Если исключить давление (пользуясь уравнением состояния), то уравнение адиабаты примет вид
TV γ – 1 = const.
При адиабатическом расширении газа (dV > 0) его давление и температура падают (dp < 0, dT < 0); при сжатии, наоборот, растут. Клеман и Дезорм в 1819 г. предложили метод измерения γ для газов, в котором используется адиабатичность их расширения при истечении через кран и для малых перепадов давления. Более точный метод определения γ связан с измерением скорости звука (адиабатическая скорость звука в идеальном газе равна a = Непосредственное определение на опыте теплоемкости cV затруднено, так как при постоянном объеме масса газа, а следовательно, и его теплоемкость малы по сравнению со значениями соответствующих величин для калориметра. Удобнее измерять теплоемкость cp и γ, а cV вычислять по формуле (15.5). Политропическим называется процесс при постоянной теплоемкости c. Частными случаями политропического процесса являются изохорический (c = cV), изобарический (c = cp), изотермический (c = ¥) и адиабатический (c = 0) процессы. Пусть теплоемкость c одного моля известна. Тогда δ Q = cdT и из первого начала в дифференциальной форме
cdT = cV dT + pdV
можно получить уравнение процесса. Итак,
(cV – c) dT + pdV = 0 ® (cV – c) / (cp – cV) × (pdV + Vdp) + pdV = 0 ®
® (cp – c) pdV + (cV – c) Vdp = 0.
Если ввести обозначение (cp – c) / (cV – c) = n (n – показатель политропы), то уравнение политропического процесса примет вид, сходный с уравнением адиабаты:
npdV + Vdp = 0 и pV n = const.
Подобным же образом могут быть получены уравнения других процессов.
|

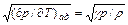 ).
).


