Примеры неравновесных процессов
В качестве иллюстрации действия сформулированных общих законов рассматривается несколько примеров. Пример 1. Показать, что энтропия идеального газа увеличивается в процессе Гей-Люссака. Пусть сосуд с жесткими адиабатическими стенками разделен перегородкой на объемы V 1 и V 2. В первом объеме ν молей идеального газа при температуре T, в другом – вакуум. Перегородка убирается – газ приходит в движение и заполняет весь объем сосуда V 1 + V 2. Это процесс Гей-Люссака. Конечное состояние газа при его расширении равновесное. Подвода теплоты нет: Q = 0. Работа внешних сил отсутствует: A ' = 0 (стенки сосуда жесткие). Внутренняя энергия газа в результате не изменится: Δ U = 0. А так как газ идеальный, то в соответствии с законом Джоуля конечная температура равна начальной температуре. Сразу же следует сделать уточнение. В процессе расширения говорить о температуре газа как целого не имеет смысла. Это неравновесный процесс, что подтверждается тем, что его конечным результатом является увеличение энтропии газа, несмотря на отсутствие подвода теплоты. Процесс протекает с конечными скоростями. Внутренняя энергия газа в процессе не остается постоянной. Она переходит в кинетическую энергию поступательного движения газа. Происходит это неравномерно. Уже с самого начала одни слои газа приходят в движение, другие еще неподвижны. Все же в конце концов кинетическая энергия движущегося газа диссипирует и переходит во внутреннюю энергию, устанавливается равновесие. Поскольку процесс неравновесный, то пользоваться уравнением (29.6) нельзя. Однако энтропия – функция состояния, ее изменение не зависит от процесса. Путей решения задачи два: можно воспользоваться полученным ранее выражением (29.5) для энтропии идеального газа и по известным начальному и конечному состояниям вычислить ее изменение. А можно реальный (неравновесный) процесс заменить подходящим равновесным (в данном случае самым простым из подходящих процессов является изотермический) и решать затем уравнение (29.6). Здесь рассматривается второй путь. Вводится изотермический процесс перехода из начального состояния с объемом V 1 в конечное состояние с объемом V 1 + V 2. В этом процессе в отличие от реального процесса есть подвод теплоты от термостата с температурой T. Эта теплота расходуется на работу газа. В результате
Δ S =
Возрастание энтропии указывает, что расширение в пустоту действительно неравновесный процесс. Пример 2. Если сосуд с водой, температура которой T, поместить в термостат с постоянной температурой Te и при этом, вообще говоря, T ≠ Te, то возникнет теплообмен, в ходе которого температура воды будет меняться, пока не сравняется с температурой термостата. Это также неравновесный процесс. В этом можно убедиться, если воспользоваться вторым началом термодинамики. Изменение энтропии воды, происходящее в результате теплообмена с термостатом, удовлетворяет неравенству (29.10):
S 2 – S 1 ≥
Это и есть второе начало термодинамики. Здесь знак равенства имеет место для равновесного процесса; строгое неравенство выполняется, если процесс неравновесный. Задача, таким образом, сводится к тому, чтобы выяснить, какой из двух вариантов реализуется. Вода имеет очень малую сжимаемость. Поэтому изменением объема воды можно пренебречь. Поскольку энтропия – функция состояния, ее изменение не зависит от процесса. Для вычисления изменения энтропии воды реальный процесс выравнивания температуры заменяется изохорическим процессом. Тогда
S 2 – S 1 =
где m – масса воды, c – ее удельная теплоемкость. От термостата к воде подводится количество теплоты
Q = cm (Te – T).
После подстановки выражений для S 2 – S 1 и Q (Te = const) приведенное выше неравенство сводится к
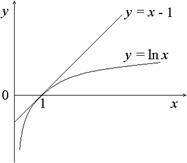
ln (Te / T) ≥ 1 – T / Te ® x = T / Te и –ln x ≥ 1 – x, или ln x ≤ x – 1.
Если на плоскости x, y построить логарифмическую кривую y = ln x и провести прямую линию y = x – 1, то из графика (рис. 14) видно, что кривая лежит ниже прямой и лишь в точке (1, 0) они касаются. Итак, равенство в (29.10) имеет место только при T = Te. Во всех остальных случаях (ниже температура воды или выше) выполняется строгое неравенство. Процесс теплообмена является неравновесным. Пример 3. Пусть сосуд с жесткими адиабатическими стенками разделен перегородкой на объемы V 1 и V 2, в которых находятся различные идеальные газы при одинаковых температуре и давлении. Перегородка убирается, происходит диффузия. Можно показать, что этот процесс также неравновесный. Здесь нет подвода теплоты, отсутствует работа внешних сил. Внутренняя энергия системы двух газов сохраняется. Отсюда следует
0 = Δ U = ν1 c V1 (T – T 0) + ν2 c V2 (T – T 0) ® T = T 0,
т. е. конечная температура смеси равна начальной температуре. Для каждого газа реальный процесс можно заменить изотермическим (как в процессе Гей-Люссака), так что
Δ Si = ν i R ln ((V 1 + V 2) / Vi), i = 1, 2.
Энтропия – аддитивная величина. Ее изменение для системы равно
Δ S = Δ S 1 + Δ S 2 = ν1 R ln (1 + V 2 / V 1) + ν2 R ln (1 + V 1 / V2) > 0. 29.16)
Пусть (для большей наглядности результата) V 1 = V 2. Тогда ν1 = ν2 = ν и
Δ S = 2 ν R ln 2 > 0.
Энтропия возросла, хотя подвода теплоты нет. Следовательно, диффузия – неравновесный процесс. Если применить теперь полученную формулу для тождественных газов, то получается парадоксальный вывод. Конечное состояние системы макроскопически ничем не отличается от начального состояния. Перегородка не играет никакой роли. Перегородку можно мысленно ставить и мысленно же убирать. Поскольку энтропия – функция состояния, ее значение для тождественных газов не должно зависеть от наличия или отсутствия перегородки. А энтропия по формуле (29.16) возрастает. Этот парадоксальный вывод получил название парадокса Гиббса. Разрешается он следующим образом. Для тождественных газов формула (29.16) неприменима, для них Δ S = 0. А формулой можно пользоваться, если молекулы или атомы газов хоть как-то различаются и смесь таких газов можно разделить на компоненты с помощью, например, центрифуги. Молекулы (атомы) одного и того же газа неразличимы, и установить, какая из частиц первоначально была в объеме V 1, а какая в объеме V 2, невозможно. От перехода неразличимых частиц из одного объема в другой макроскопическое состояние системы не меняется. Закон возрастания энтропии не означает, что энтропия какой-либо части изолированной или адиабатически изолированной системы не может уменьшаться. Во втором из рассмотренных примеров сложная система "вода + термостат" является изолированной. В ней идет неравновесный процесс теплообмена между водой и термостатом. Знаки изменения энтропии воды и термостата противоположные. Если энтропия воды возрастает, то энтропия термостата убывает, и наоборот. Энтропия системы в целом увеличивается. В циклической тепловой машине энтропия нагревателя уменьшается из-за передачи теплоты рабочему телу. Энтропия рабочего тела оказывается равной первоначальной по завершении цикла. Роль холодильника заключается в увеличении энтропии, по крайней мере, настолько, насколько уменьшается энтропия нагревателя. Передача части теплоты холодильнику есть плата за то, чтобы другая часть теплоты циклической тепловой машиной превращалась в работу. Максимальный к. п. д. тепловой машины достигается, когда увеличение энтропии холодильника равно уменьшению энтропии нагревателя.
|

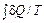 =
= 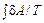 =
= 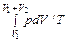 = ν R· ln (1 + V 2 / V 1) > 0.
= ν R· ln (1 + V 2 / V 1) > 0. .
.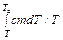 = cm ×ln (Te / T),
= cm ×ln (Te / T),