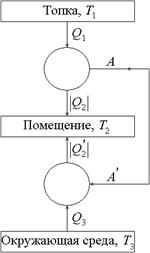
Динамический способ отопления помещения
В качестве примера на применение неравенства Клаузиуса рассматривается проблема динамического отопления помещения. В обычном способе отопления теплота, выделяющаяся при сгорании топлива, непосредственно поступает в отапливаемое помещение. Значительная доля этой теплоты уносится нагретыми газами и бесполезно расходуется на нагрев окружающей среды. Но даже если отвлечься от этой и других потерь, помещение при обычном способе обогрева получает теплоты не больше, чем выделяется при сгорании топлива. При динамическом способе отопления только часть теплоты от сгорания топлива поступает в помещение, другая же часть расходуется на работу тепловой машины. С ее помощью приводится в действие холодильная машина, которая отбирает теплоту у окружающей среды и передает ее в помещение. Таким образом, помещение получает теплоту и от топки, и от холодной окружающей среды. Общее количество теплоты, получаемое помещением, может оказаться больше, чем выделяющееся при сгорании топлива. В этом выгода данного способа отопления. Он был предложен В. Томсоном. Схематично динамический способ отопления изображен на рис. 13. Пусть T 1, T 2 и T 3 – температуры топки, помещения и окружающей среды соответственно. Количество теплоты, получаемое при сгорании топлива, равно Q 1. Оно расходуется на работу A тепловой машины, часть его ÷ Q 2÷ (Q 2 < 0) поступает в помещение. Очевидно, A ≤ Q 1 – ÷ Q 2÷ (из-за возможных потерь части теплоты). Этой работой приводится в действие холодильная машина. Здесь возможны тоже потери на трение и т. д. Поэтому A ≥ A '. Холодильная машина отбирает от окружающей среды теплоту Q 3 и передает помещению теплоту ÷ Q 2'÷ (Q 2' < 0). Здесь имеет место неравенство A ' + Q 3 ≥ ÷ Q 2'÷. Из этих неравенств получается Q 1 – ÷ Q 2÷ ≥ ÷ Q 2'÷ – Q 3, или Q 3 ≥ (÷ Q 2÷ + ÷ Q 2'÷) – Q 1. В скобках теплота, поступающая в отапливаемое помещение. Если обозначить ее через Q (Q = ÷ Q 2÷ + ÷ Q 2'÷), то Q 3 ≥ Q – Q 1. Если теперь рассмотреть тепловую и холодильную машины как одну термодинамическую систему, совершающую циклический процесс, то на основании неравенства Клаузиуса
Q 1 / T 1 + (Q 2 + Q 2') / T 2 + Q 3 / T 3 ≤ 0,
и с учетом того, что Q 2 = – ÷ Q 2÷ и Q 2' = – ÷ Q 2'÷, получается
Q 1 / T 1 – (÷ Q 2÷ + ÷ Q 2'÷) / T 2 + Q 3 / T 3 ≤ 0,
или
Q 1 / T 1 – Q / T 2 + Q 3 / T 3 ≤ 0.
Исключение Q 3 дает Q 1 / T 1 – Q / T 2 + (Q – Q 1) / T 3 ≤ 0,
откуда
Q ≤ (T 3–1 – T 1–1) / (T 3–1 – T 2–1) × Q 1.
В идеальном случае, когда какие-либо потери теплоты или работы отсутствуют и все процессы квазистатические, имеет место равенство
Q = (T 3–1 – T 1–1) / (T 3–1 – T 2–1) × Q 1.
Так как T 1 > T 2, то T 3–1 – T 1–1 > T 3–1 – T 2–1 и полученная формула дает Q > Q 1. Более того, разница температур T 2 и T 3 сравнительно небольшая (до нескольких десятков градусов), тогда как T 1 значительно больше T 2 (на сотни градусов). Поэтому множитель перед Q 1 может быть порядка 10. Это говорит об эффективности динамического способа отопления.
|