Термодинамическое определение энтропии
Для квазистатических циклических процессов неравенство Клаузиуса переходит в равенство
где T – температура системы, равная температуре окружающей среды в момент получения системой количества теплоты δ Q. Из этого равенства следует, что для всякого квазистатического, не циклического процесса значение интеграла
Изменение направления интегрирования во втором слагаемом дает
Количество теплоты, полученное системой, деленное на температуру, при которой оно было получено, иногда называют приведенным количеством теплоты. Пользуясь этой терминологией, можно сказать: приведенное количество теплоты, квазистатически полученное системой, не зависит от пути перехода, а определяется лишь начальным и конечным состояниями системы. Приведенная теплота термин исторический. Им редко пользуются. Тот факт, что при квазистатическом переходе значение интеграла
S = S 0 +
Ее называют энтропией. Энтропия определяется с точностью до произвольной постоянной. Однако в термодинамике смысл имеет не сама энтропия, а ее изменение (разность значений энтропии в двух состояниях). Условно энтропию в каком-либо состоянии можно принять за нуль, определяя тем самым указанную постоянную. В случае идеального газа интеграл в (29.3) легко вычисляется. По первому началу
δ Q = dU + pdV.
Для идеального газа
dU = ν cVdT, а p = ν RT / V.
Поэтому
S = ν ( или S = ν ( Выражение в скобках дает энтропию одного моля. Она не зависит от числа молей и, стало быть, от числа частиц; это функция температуры и молярного объема V / ν (cV – молярная теплоемкость). Энтропия всего газа (в объеме V) пропорциональна числу молей. Если теплоемкость cV постоянна, то, используя соотношение Майера и уравнение Клапейрона–Менделеева, можно выражение (29.4) преобразовать к виду
S = S 0 + ν cV ln (pV γ/ p 0 V 0 γ), (29.5)
где S 0 – значение энтропии при p = p 0 и V = V 0. Знакомое по предыдущему уравнение адиабаты для идеального газа получается из выражения (29.5) непосредственно. Если объем теплоизолирован, то энтропия содержащегося в нем газа при равновесных изменениях состояния остается постоянной. Тогда из выражения (29.5) следует уравнение адиабатического процесса для идеального газа:
pV γ = const.
Для нахождения энтропии произвольной системы в некотором состоянии надо систему перевести в это состояние каким-либо равновесным путем, безразлично каким именно, из состояния, в котором энтропия известна. Несколько позже эта методика будет продемонстрирована на конкретных примерах: разлет газа в пустоту, теплообмен и др. Изменение энтропии системы при бесконечно малом теплоподводе в соответствии с определением (29.3) равно
dS = δ Q / T. (29.6)
Это приращение энтропии в отличие от бесконечно малого количества подводимой теплоты δ Q является полным дифференциалом. Интегрирующим множителем служит 1/ T. Очевидно, для любого квазистатического циклического процесса
Уравнение (29.6) является математическим выражением второго начала термодинамики для равновесных процессов. Из уравнений (29.6) и (10.3) получается фундаментальное уравнение, объединяющее первое и второе начала термодинамики
dU = TdS – δ A + δ Z. (29.8)
Оно имеет место только для равновесных (квазистатических) процессов. Его часто называют основным термодинамическим тождеством. Для определенной массы газа (или иной какой-либо сжимаемой среды при наличии лишь сил давления) это уравнение принимает вид
dU = TdS – pdV. (29.9)
Энтропия относится к экстенсивным величинам. Действительно, количество теплоты, поглощаемое системой на каждой стадии процесса при переходе из исходного состояния в рассматриваемое состояние, пропорционально массе. Поэтому энтропия также пропорциональна массе. Для идеального газа это показано выше. Если система состоит из термически равновесных подсистем, то ее энтропия равна сумме энтропий подсистем (энтропия – аддитивная функция состояния).
|

 = 0, (29.1)
= 0, (29.1)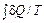 не зависит от пути, по которому происходит процесс. Действительно, пусть система может переходить из состояния 1 в состояние 2 различными способами, каждый из которых является квазистатическим процессом. Если взять из них два произвольных (пусть это будут процессы a и b) и объединить их в один квазистатический циклический процесс, то для него можно написать равенство (29.1)
не зависит от пути, по которому происходит процесс. Действительно, пусть система может переходить из состояния 1 в состояние 2 различными способами, каждый из которых является квазистатическим процессом. Если взять из них два произвольных (пусть это будут процессы a и b) и объединить их в один квазистатический циклический процесс, то для него можно написать равенство (29.1) = 0.
= 0.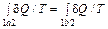 . (29.2)
. (29.2)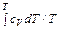 + R
+ R 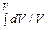 + const),
+ const), = 0. (29.7)
= 0. (29.7)


