В ультраразреженном газе по-иному протекают и явления переноса. Понятие локального равновесия теряет смысл.

|
| Рис. 46
|
Пусть между двумя параллельными стенками, имеющими температуру  , находится ультраразреженный газ (рис. 46). В стационарных условиях из j молекул, ежесекундно ударяющихся о стенку,
, находится ультраразреженный газ (рис. 46). В стационарных условиях из j молекул, ежесекундно ударяющихся о стенку, 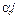 прилипает к ней и столько же молекул испаряется, унося с собой среднюю энергию, соответствующую температуре стенки. Наряду с ними имеются
прилипает к ней и столько же молекул испаряется, унося с собой среднюю энергию, соответствующую температуре стенки. Наряду с ними имеются 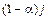 молекул, которые упруго отражаются от стенки и сохраняют свою энергию неизменной. Таким образом, между стенками в каждом из двух противоположных направлений движутся молекулы, обладающие средними энергиями, соответствующие температурам разных стенок, причем
молекул, которые упруго отражаются от стенки и сохраняют свою энергию неизменной. Таким образом, между стенками в каждом из двух противоположных направлений движутся молекулы, обладающие средними энергиями, соответствующие температурам разных стенок, причем
 . (107.1)
. (107.1)
Здесь верхние индексы "+" и "–" означают направление движения, нижние "1" и "2" – номер стенки, в равновесии с которой находятся молекулы. Создаваемый этими молекулами поток тепла равен
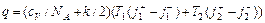 . (107.2)
. (107.2)
В этом выражении для q учитывается, что молекулы в потоке обладают более высокой средней энергией (на величину kT / 2 каждая).
Потоки молекул удовлетворяют балансовым соотношениям
 (107.3)
(107.3)
Не все эти соотношения являются независимыми – сложение уравнений каждой системы дает j. Из них и определения j следует, что
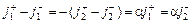 ,
,
откуда  , и с учетом соотношений (107.1) и (107.3)
, и с учетом соотношений (107.1) и (107.3) 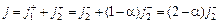 . В результате
. В результате
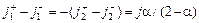 . (107.4)
. (107.4)
Поскольку каждый из потоков 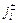 (i = 1, 2) формируется при отражении от плоской поверхности практически бесконечных размеров, то распределение соответствующих молекул по направлениям движения можно приближенно считать равномерным. Иными словами, для связи
(i = 1, 2) формируется при отражении от плоской поверхности практически бесконечных размеров, то распределение соответствующих молекул по направлениям движения можно приближенно считать равномерным. Иными словами, для связи 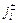 с
с 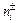 можно воспользоваться формулой (86.3):
можно воспользоваться формулой (86.3):
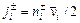 . (107.5)
. (107.5)
Здесь деление производится на два (а не на четыре) в связи с тем, что 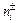 – концентрации молекул, летящих в полусферу. Исключение из соотношений (107.1), (107.3) и (107.5) величин с верхними индексами дает
– концентрации молекул, летящих в полусферу. Исключение из соотношений (107.1), (107.3) и (107.5) величин с верхними индексами дает
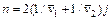 . (107.6)
. (107.6)
С помощью соотношений (107.4), (107.6) выражение (107.2) для q может быть преобразовано к виду
 (107.7)
(107.7)
Поток тепла в ультраразреженном газе линейным образом зависит от плотности газа.
Аналогично может быть рассмотрено молекулярное течение между двумя параллельными пластинами, движущихся вдоль самих себя в одном направлении. Для силы трения получается выражение
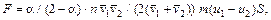 (107.8)
(107.8)
где S – площадь пластины. Если температуры пластин одинаковы и  (a называют коэффициентом аккомодации), то формула (107.8) упрощается:
(a называют коэффициентом аккомодации), то формула (107.8) упрощается:
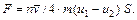 (107.9)
(107.9)

|
|
Рис. 47
|
Физический смысл результата прозрачен: о единицу поверхности в единицу времени ударяется 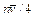 молекул, каждая из них передает верхней пластине импульс
молекул, каждая из них передает верхней пластине импульс  График силы трения F для всего диапазона плотности газа n (концентрации) показан на рис. 47, где
График силы трения F для всего диапазона плотности газа n (концентрации) показан на рис. 47, где  определяется из условия
определяется из условия 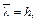 F 0 – значение силы трения для высоких плотностей. Такой же вид имеет графическая зависимость потока тепла q от n.
F 0 – значение силы трения для высоких плотностей. Такой же вид имеет графическая зависимость потока тепла q от n.


 , находится ультраразреженный газ (рис. 46). В стационарных условиях из j молекул, ежесекундно ударяющихся о стенку,
, находится ультраразреженный газ (рис. 46). В стационарных условиях из j молекул, ежесекундно ударяющихся о стенку, 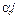 прилипает к ней и столько же молекул испаряется, унося с собой среднюю энергию, соответствующую температуре стенки. Наряду с ними имеются
прилипает к ней и столько же молекул испаряется, унося с собой среднюю энергию, соответствующую температуре стенки. Наряду с ними имеются 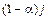 молекул, которые упруго отражаются от стенки и сохраняют свою энергию неизменной. Таким образом, между стенками в каждом из двух противоположных направлений движутся молекулы, обладающие средними энергиями, соответствующие температурам разных стенок, причем
молекул, которые упруго отражаются от стенки и сохраняют свою энергию неизменной. Таким образом, между стенками в каждом из двух противоположных направлений движутся молекулы, обладающие средними энергиями, соответствующие температурам разных стенок, причем . (107.1)
. (107.1)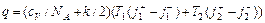 . (107.2)
. (107.2) (107.3)
(107.3)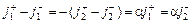 ,
, , и с учетом соотношений (107.1) и (107.3)
, и с учетом соотношений (107.1) и (107.3) 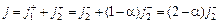 . В результате
. В результате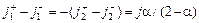 . (107.4)
. (107.4)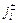 (i = 1, 2) формируется при отражении от плоской поверхности практически бесконечных размеров, то распределение соответствующих молекул по направлениям движения можно приближенно считать равномерным. Иными словами, для связи
(i = 1, 2) формируется при отражении от плоской поверхности практически бесконечных размеров, то распределение соответствующих молекул по направлениям движения можно приближенно считать равномерным. Иными словами, для связи 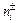 можно воспользоваться формулой (86.3):
можно воспользоваться формулой (86.3):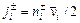 . (107.5)
. (107.5)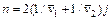 . (107.6)
. (107.6) (107.7)
(107.7)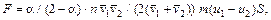 (107.8)
(107.8) (a называют коэффициентом аккомодации), то формула (107.8) упрощается:
(a называют коэффициентом аккомодации), то формула (107.8) упрощается: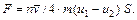 (107.9)
(107.9)
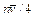 молекул, каждая из них передает верхней пластине импульс
молекул, каждая из них передает верхней пластине импульс  График силы трения F для всего диапазона плотности газа n (концентрации) показан на рис. 47, где
График силы трения F для всего диапазона плотности газа n (концентрации) показан на рис. 47, где  определяется из условия
определяется из условия 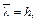 F 0 – значение силы трения для высоких плотностей. Такой же вид имеет графическая зависимость потока тепла q от n.
F 0 – значение силы трения для высоких плотностей. Такой же вид имеет графическая зависимость потока тепла q от n.


