Решение. 1. Находим образы векторов :
1. Находим образы
Итак, образы базисных векторов базиса
Для составления матрицы
Составляем матрицу
2) Для нахождения ядра
оператора необходимо решить однородную систему уравнений
с основной матрицей Выписываем матрицу
Переходя от ступенчатой матрицы к системе уравнений, получим
Так как ранг ступенчатой матрицы равен 2, система имеет бесконечное множество решений. В качестве базисных (основных) переменных выберем переменные
Итак, ядро
Взяв
Так как базис ядра состоит из одного вектора, то размерность ядра (дефект оператора) равен 1:
Размерность образа оператора (ранг оператора) равна
Для нахождения базиса образа
|
векторов 
:
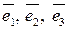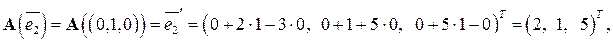
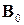имеют вид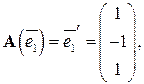
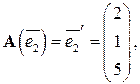
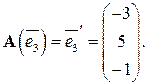
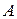линейного оператора 
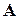в базисе 
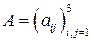линейного оператора, столбцами которой являются коэффициенты разложения векторов 
.
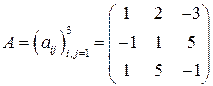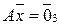
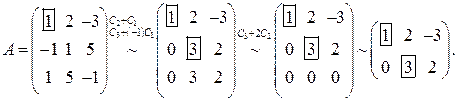
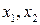(при этом 
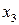является свободной переменной). Выражая базисные переменные 
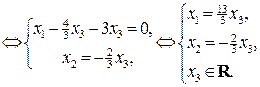
оператора состоит из всех векторов вида
.
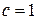, получим базис в ядре, состоящий из одного вектора
.
.
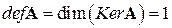
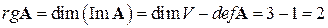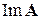достаточно взять из векторов 
