(матрицы линейного оператора)
Напомним основные понятия лекции “Собственные значения и собственные векторы линейного оператора”.
Пусть в линейном пространстве  задан линейный оператор
задан линейный оператор  .
.
Определение. Ненулевой вектор  , удовлетворяющий условию (операторному равенству)
, удовлетворяющий условию (операторному равенству)
 ,
, 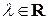 , (1)
, (1)
называется собственным вектором оператора 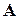 . Число
. Число 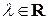 при этом называется собственным значением (собственным числом) оператора
при этом называется собственным значением (собственным числом) оператора 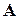 , соответствующим собственному вектору
, соответствующим собственному вектору  .
.
Выберем в пространстве  некоторый базис
некоторый базис 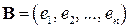 и пусть оператору
и пусть оператору 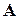 в этом базисе соответствует матрица
в этом базисе соответствует матрица  . Тогда операторное равенство (1) можно переписать в матричном виде
. Тогда операторное равенство (1) можно переписать в матричном виде
 ,
,  ,
,
или в виде системы уравнений
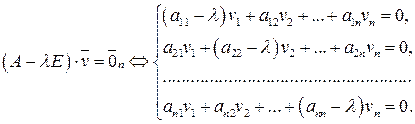 (2)
(2)
Так как нас интересуют нетривиальные решения системы (2) (поскольку собственный вектор по определению должен быть ненулевым), то основная матрица  системы (2)должна быть вырожденной, то есть
системы (2)должна быть вырожденной, то есть
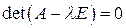 .
.
Определение. Уравнение
 (3)
(3)
называется характеристическим уравнением оператора 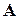 .
.
Разложив определитель  в уравнении (3), получим многочлен
в уравнении (3), получим многочлен
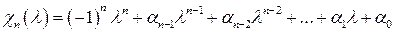 (4)
(4)
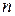 -ой степени относительно
-ой степени относительно  . Многочлен (4) называется характеристическим многочленом оператора
. Многочлен (4) называется характеристическим многочленом оператора 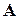 , его корни – характеристическими корнями многочлена (4).
, его корни – характеристическими корнями многочлена (4).
Теорема. Для того чтобы число 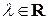 являлось собственным значением линейного оператора
являлось собственным значением линейного оператора 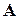 , необходимо и достаточно, чтобы оно было корнем характеристического уравнения (3) этого оператора.
, необходимо и достаточно, чтобы оно было корнем характеристического уравнения (3) этого оператора.
Определение. Алгебраической кратностью собственного значения  линейного оператора
линейного оператора 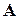 называется кратность корня
называется кратность корня  характеристического уравнения (3) (кратность характеристического многочлена
характеристического уравнения (3) (кратность характеристического многочлена  ).
).
Кратностью корня  называется натуральное число
называется натуральное число  такое, что
такое, что
 ,
,  , …,
, …,  ,
, 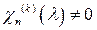 .
.

 задан линейный оператор
задан линейный оператор  .
. , удовлетворяющий условию (операторному равенству)
, удовлетворяющий условию (операторному равенству) ,
, 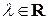 , (1)
, (1)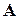 . Число
. Число 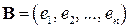 и пусть оператору
и пусть оператору  . Тогда операторное равенство (1) можно переписать в матричном виде
. Тогда операторное равенство (1) можно переписать в матричном виде ,
,  ,
,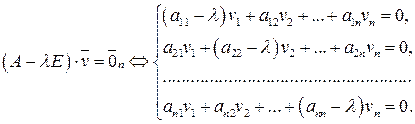 (2)
(2) системы (2)должна быть вырожденной, то есть
системы (2)должна быть вырожденной, то есть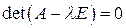 .
. (3)
(3) в уравнении (3), получим многочлен
в уравнении (3), получим многочлен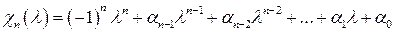 (4)
(4)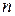 -ой степени относительно
-ой степени относительно  . Многочлен (4) называется характеристическим многочленом оператора
. Многочлен (4) называется характеристическим многочленом оператора  ).
). такое, что
такое, что ,
,  , …,
, …,  ,
, 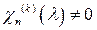 .
.


