Tpигонометрична форма к.ч.
Нехай відомі модуль У випадку розміщення осей
Остання форма запису комплексного числа називається тригонометричною. Як бачимо, щоб знайти тригонометричну форму, досить обчислити модуль і аргумент к.ч. Приклади. Записати в тригонометричній формі слідуючі числа: 1) Розв’язання 1) Відповідь: 2) Відповідь: 3) Відповідь: Розглянемо алгоритм переходу від алгебраїчної до тригонометричної форми к.ч. Нехай дано к.ч. 1. Побудувати на площині ХОУ к.ч.
2. Знаходимо модуль к.ч.
На прикладі маємо:
3. За допомогою таблиць або мікрокалькулятора знаходимо
На прикладі: 4. За формулою (1.1) § 1.14 знаходимо
5. Підставимо знайдені
Для
Приклади для самостійного розв’язання Представити у тригонометричній формі числа: 1. Відповіді. 1. 2. 3. 4.
4.16. Множення і ділення к.ч. в тригонометричній формі Нехай числа Справедливі слідуючі формули:
Таким чином, при множенні (діленні) к.ч. їх модулі множаться (діляться), а аргументи додаються (віднімаються). З’ясуємо геометричний зміст множення. Нехай Отже, множення к.ч. зводиться до повороту і розтягу (стиску) векторів. Подібний зміст має і ділення к.ч.
Приклад. Використовуючи тригонометричну форму, обчислити добуток чисел Розв’язання. З геометричної точки зору були виконані слідуючі перетворення (рис.1.9): 1) поворот вектора 2) стиск (без зміни напряму) вектора
Рис.1.9 За допомогою рис.1.9 в даному випадку легко перевірити, що Приклади для самостійного розв’язання 1. Дані числа 1) перетворити їх у тригонометричну форму; 2) знайти їх добуток 3) частку 4) зробити перевірку, виконавши ці дії над 2. Задовольнити умови прикладу 1, якщо Відповіді. 1. 1) 2) 3) 2. 1) 2) 3)
4.17. Формула піднесення к.ч.до цілого степеня n
(Формула Муавра): якщо
Приклад. Нехай Розв’язання. Подамо
Приклади для самостійного розв’язання Обчислити: 1. Відповіді. 1.
4.18. Формула добування коренів
Формула добування коренів
де Таким чином, Приклад. Знайти всі значення Розв’язання. Запишемо число 8 в тригонометричній формі:
Одержуємо три значення кореня:
Приклади для самостійного розв’язання Знайти всі значення коренів: 1. Відповіді. 1. k= 1: k= 2: 2. = При k= 0: k= 1: k= 2: k= 3: 3. де k= 0, 1, 2, 3, 4, 5.
|

 і аргумент
і аргумент  к.ч.
к.ч. 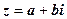 (див рис.1.5). Зауважимо, що
(див рис.1.5). Зауважимо, що  - полярні координати точки
- полярні координати точки 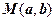 , яка зображає число
, яка зображає число 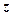 (якщо
(якщо 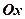 - полярна вісь).
- полярна вісь). , вказаному на рис. 1.5, відомі формули переходу від полярних до прямокутних координат точки
, вказаному на рис. 1.5, відомі формули переходу від полярних до прямокутних координат точки  . Додамо ці рівності, помноживши другу на
. Додамо ці рівності, помноживши другу на  :
: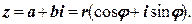
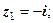 2)
2)  3)
3) 

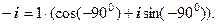

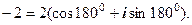

 .
. . Для переходу до тригонометричної форми необхідно:
. Для переходу до тригонометричної форми необхідно: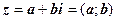 і встановити, до якої чверті належить
і встановити, до якої чверті належить  . На даному прикладі:
. На даному прикладі: 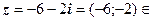 ІІІ четв. Див. рис.
ІІІ четв. Див. рис.
 (1)
(1)
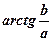 , ураховуючи при цьому властивість
, ураховуючи при цьому властивість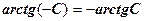 .
.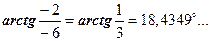 .
. . Для даного прикладу:
. Для даного прикладу:  ІІІ чверті. Маємо:
ІІІ чверті. Маємо: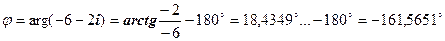
 і
і  (2)
(2) маємо:
маємо:
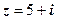 2.
2.  3.
3.  4.
4. 




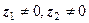 записані в тригонометричній формі:
записані в тригонометричній формі:  .
.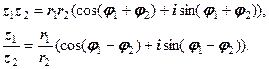
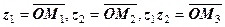 (рис 1.8). Очевидно, що
(рис 1.8). Очевидно, що  одержано поворотом
одержано поворотом  на кут
на кут 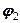 з подальшим розтягом (стиском)
з подальшим розтягом (стиском)  разів.
разів.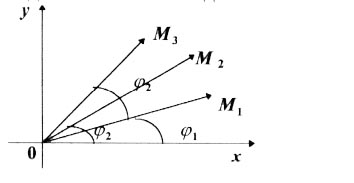
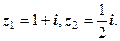 З’ясувати геометричний зміст операції множення цих чисел.
З’ясувати геометричний зміст операції множення цих чисел.

 на кут
на кут  результат повороту;
результат повороту; в 2 рази
в 2 рази  - результат множення.
- результат множення.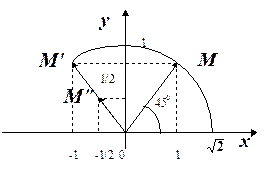
 .
.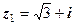 та
та  . Необхідно:
. Необхідно: ;
;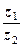 ;
;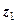 і
і  в алгебраїчній формі.
в алгебраїчній формі. ,
, 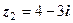 .
.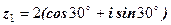 ,
,  ;
; ;
;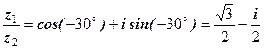 .
. ,
,  ;
; ;
; .
. то
то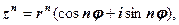 (1.3)
(1.3) . Обчислити
. Обчислити 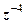 .
.

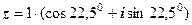 застосовуємо формулу (1.3) при
застосовуємо формулу (1.3) при  :
:
 2.
2.  3.
3. 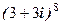
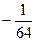 . 2. –1. 3. 104976.
. 2. –1. 3. 104976. го степеня з числа
го степеня з числа 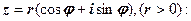
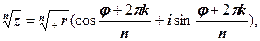 (1.4)
(1.4) символ
символ  означає корінь арифметичний з дійсного числа
означає корінь арифметичний з дійсного числа  .
. при
при 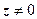 має точно
має точно  значень.
значень. .
. Застосовуємо формулу (1.4) при
Застосовуємо формулу (1.4) при 
 де
де 
 Відповідь:
Відповідь: 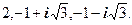
 2.
2.  3.
3. 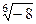 .
.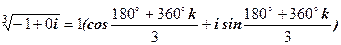 ,де k= 0, 1, 2. При k= 0:
,де k= 0, 1, 2. При k= 0: 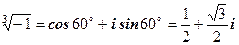 ;
;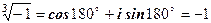 ;
;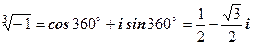 .
.
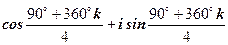 , де k= 0, 1, 2, 3.
, де k= 0, 1, 2, 3.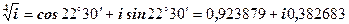 ;
; ;
; ;
;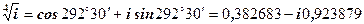 .
.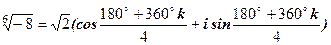 ,
,


