У вибраній прямокутній системі координат число 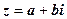 зображається точкою
зображається точкою 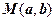 (рис.1.1). Навпаки, якщо задана точка
(рис.1.1). Навпаки, якщо задана точка 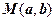 , то їй співставляється к.ч.
, то їй співставляється к.ч. 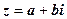 . Таким чином, між множиною к.ч. і множиною точок площини (з заданою прямокутною системою координат) встановлюється взаємно однозначна відповідність.
. Таким чином, між множиною к.ч. і множиною точок площини (з заданою прямокутною системою координат) встановлюється взаємно однозначна відповідність.
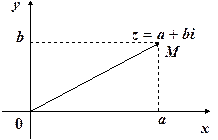
Рис.1.1.
Очевидно, що дійсні числа зображуються точками на осі 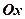 , а чисто уявні - на осі
, а чисто уявні - на осі  ; з цієї причини
; з цієї причини  називають дійсною, а
називають дійсною, а  – уявною віссю; площину
– уявною віссю; площину  називають комплексною площиною, а к.ч. - точками цієї площини.
називають комплексною площиною, а к.ч. - точками цієї площини.
Приклади. Знайти множину к.ч., що задовольняють умову:
 ;
;
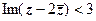 .
.
Розв’язання.
1) Нехай 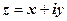 . Умову перепишемо в рівносильній формі:
. Умову перепишемо в рівносильній формі: 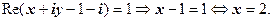
Відповідь: множина чисел  пряма
пряма 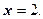
2) Якщо 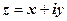 , то,
, то, 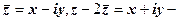
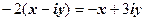 , отже,
, отже, 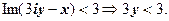
Відповідь: множина чисел 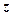 - півплощина, що розміщена нижче прямої
- півплощина, що розміщена нижче прямої 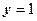 .
.
Побудувати на площині ХОУ к.ч., записати їх дійсну та уявну частину. Обчислити модулі к.ч.
1.  . 2.
. 2.  . 3.
. 3. 
Відповіді. 1. 


2. 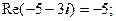
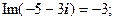
 .
.
3. 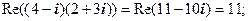
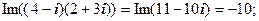
 .
.
4.10. Коло, круг, кільце
Нехай дано числа 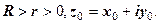
Рівнянню 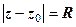 задовольняють всі числа (і тільки вони), що розміщені на колі радіуса
задовольняють всі числа (і тільки вони), що розміщені на колі радіуса 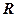 з центром у точці
з центром у точці 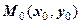 . Дійсно, якщо
. Дійсно, якщо 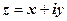 , то
, то 
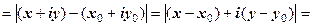
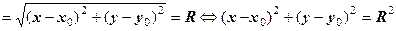 .
.
Очевидно, що нерівності 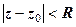 і
і 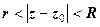 задають відповідно круг і кільце. На рис. 1.2 зображено кільце
задають відповідно круг і кільце. На рис. 1.2 зображено кільце 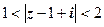 з центром у точці
з центром у точці 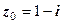 .
.
Звернемо увагу на вироджені випадки кільця 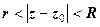 :
:
(1) 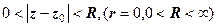 – круг з виключеним центром
– круг з виключеним центром 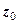 ;
;
(2) 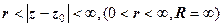 – зовнішність круга
– зовнішність круга  – круг з границею;
– круг з границею;
(3) 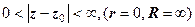 – вся площина з виключеною точкою
– вся площина з виключеною точкою 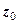 ;
;
(4) при  маємо пусту множину.
маємо пусту множину.

Рис. 1.2
Приклад. З’ясувати, чи належить точка 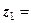 p до круга
p до круга  .
.
Розв’язання. Порівняємо радіус  з відстанню
з відстанню  від центра круга
від центра круга  до точки
до точки 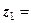 p:
p:
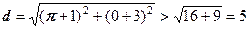 .
.
Відповідь: точка 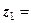 p розміщена поза кругом.
p розміщена поза кругом.

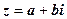 зображається точкою
зображається точкою 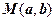 (рис.1.1). Навпаки, якщо задана точка
(рис.1.1). Навпаки, якщо задана точка 
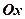 , а чисто уявні - на осі
, а чисто уявні - на осі  ; з цієї причини
; з цієї причини 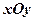 називають комплексною площиною, а к.ч. - точками цієї площини.
називають комплексною площиною, а к.ч. - точками цієї площини. ;
;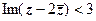 .
.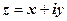 . Умову перепишемо в рівносильній формі:
. Умову перепишемо в рівносильній формі: 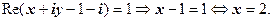
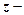 пряма
пряма 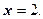
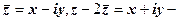
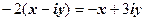 , отже,
, отже, 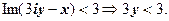
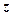 - півплощина, що розміщена нижче прямої
- півплощина, що розміщена нижче прямої 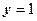 .
. . 2.
. 2.  . 3.
. 3. 



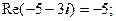
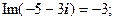
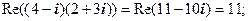
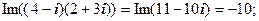
 .
.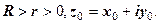
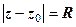 задовольняють всі числа (і тільки вони), що розміщені на колі радіуса
задовольняють всі числа (і тільки вони), що розміщені на колі радіуса 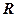 з центром у точці
з центром у точці 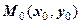 . Дійсно, якщо
. Дійсно, якщо 
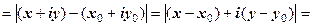
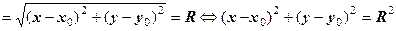 .
.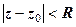 і
і 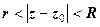 задають відповідно круг і кільце. На рис. 1.2 зображено кільце
задають відповідно круг і кільце. На рис. 1.2 зображено кільце 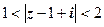 з центром у точці
з центром у точці 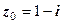 .
.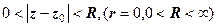 – круг з виключеним центром
– круг з виключеним центром 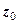 ;
;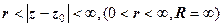 – зовнішність круга
– зовнішність круга  – круг з границею;
– круг з границею;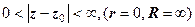 – вся площина з виключеною точкою
– вся площина з виключеною точкою  маємо пусту множину.
маємо пусту множину.
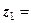 p до круга
p до круга  .
. з відстанню
з відстанню  від центра круга
від центра круга  до точки
до точки 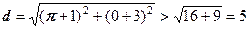 .
.


