Свойства комплексных чисел
Глава 1. Комплексные числа Основные понятия
Первоначальные данные о числе относятся к эпохе каменного века – палеомелита. Это «один», «мало» и «много». Записывались они в виде зарубок, узелков и т.д. Развитие трудовых процессов и появление собственности заставили человека изобрести числа и их названия. Первыми появились натуральные числа N, получаемые при счете предметов. Затем, наряду с необходимостью счета, у людей появилась потребность измерять длины, площади, объемы, время и другие величины, где приходилось учитывать и части употребляемой меры. Так возникли дроби. Формальное обоснование понятий дробного и отрицательного числа было осуществлено в 19 веке. Множество целых чисел Z – это натуральные числа, натуральные со знаком минус и нуль. Целые и дробные числа образовали совокупность рациональных чисел Q, но и она оказалась недостаточной для изучения непрерывно изменяющихся переменных величин. Бытие снова показало несовершенство математики: невозможность решить уравнение вида х 2 = 3, в связи с чем появились иррациональные числа I. Объединение множества рациональных чисел Q и иррациональных чисел I – множество действительных (или вещественных) чисел R. В итоге числовая прямая заполнилась: каждому действительному числу соответствовала на ней точка. Но на множестве R нет возможности решить уравнение вида х 2 = – а 2. Следовательно, снова возникла необходимость расширения понятия числа. Так в 1545 году появились комплексные числа. Их создатель Дж. Кардано называл их «чисто отрицательными». Название «мнимые» ввел в 1637 году француз Р. Декарт, в 1777 году Эйлер предложил использовать первую букву французского числа i для обозначения мнимой единицы. Этот символ вошел во всеобщее употребление благодаря К. Гауссу. В течение 17 – 18 веков продолжалось обсуждение арифметической природы мнимостей, их геометрического истолкования. Датчанин Г. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изображать комплексное число точкой на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой, а вектором, идущим в эту точку из начала координат. Лишь к концу 18 – началу 19 века комплексные числа заняли достойное место в математическом анализе. Первое их использование – в теории дифференциальных уравнений и в теории гидродинамики.
Определение 1. Комплексными числами называются упорядоченные пары действительных чисел (x, y), для которых определены равенства и операции сложения и умножения по следующим правилам: 1) (x 1, y 1) = (x 2, y 2) тогда и только тогда, когда x 1 = x 2, y 1 = y 2, 2) (x 1, y 1) + (x 2, y 2) = (x 1 + x 2, y 1 + y 2), 3) (x 1, y 1) · (x 2, y 2) = (x 1 x 2 – y 1 y 2, x 1 y 2 + x 2 y 1).
Обозначение комплексного числа z = (x, y), множества всех комплексных чисел – С. Свойства комплексных чисел 1. Переместительный закон сложения: z 1 + z 2 = z 2 + z 1 2. Ассоциативный или сочетательный закон: z 1 + (z 2 + z 3) = (z 1 + z 2) + z 3 3. Переместительный закон умножения: z 1 · z 2 = z 2 · z 1 4. Распределительный закон: z 1 · (z 2 + z 3) = z 1 z 2 + z 1 z 3 Операции вычитания и деления вводятся как обратные к операциям сложения и умножения: – разностью двух чисел z 1 и z 2 называется число z 3 такое, что сумма z 3 и z 2 равна z 1, т.е. z 1 – z 2 = z 3: z 1 = z 2 + z 3, – частным двух чисел z 1 и z 2 называется число z 3 такое, что произведение z 3 и z 2 равно z 1, т.е. Определение 2. Комплексным нулем называется число z = (0, 0). Для каждого комплексного числа вида z = (x, 0)справедливо, что z = (x, 0) = х, где Следовательно, любое действительное число можно представить в виде комплексного числа, т.е Определение 3. Сопряженным к комплексному числу z = (x, y) называется комплексное число Определение 4. Мнимой единицей называется комплексное число z = (0, 1) = i. i 2 = – 1. Пояснение: i 2 = (0, 1) · (0, 1) = (по правилу 3 определения 1) = (0·0 –1·1, 0·1 + 1·0) = (–1, 0) = (по определению (x, 0) = х) = – 1. Для каждого комплексного числа вида (0, y) справедливо, что (0, y) = iy, где Парой действительных чисел (x, y) обозначаются координаты точки на плоскости или координаты вектора, т.е. между множеством векторов на плоскости и множеством комплексных чисел можно установить взаимно-однозначное соответствие: При таком истолковании сложению и вычитанию комплексных чисел соответствуют эти же операции над векторами. Определение 5. Действительной частью комплексного числа z = (x, y) называется действительное число х. Обозначение: x = Re z (от латинского Realis). Определение 6. Мнимой частью комплексного числа z = (x, y) называется действительное число y. Обозначение: y = Im z (от латинского Imaginarius).
Re z откладывается на оси (Ох), Im z откладывается на оси (Оy), тогда вектор
Определение 7. Плоскость, точкам которой поставлено в соответствие множество комплексных чисел, называется комплексной плоскостьюили плоскостью Гаусса. Обозначение – (z), С. Определение 8. Модулем комплексного числа z = (x, y) называется длина вектора
Определение 9. Аргументом комплексного числа z = (x, y) называется угол между положительным направлением оси (Ох) и вектором Из рисунка 1 видно, что Определение 10. Главным значением Аргумент комплексного числа находится по формуле:
Замечание 1. Аргумент комплексного числа определяется неоднозначно. Всякий угол, отличающийся от Замечание 2. В некоторых задачахглавным значением
|

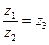 : z 1 = z 2 · z 3.
: z 1 = z 2 · z 3. .
.

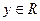 , так как (0, y) = (0, 1) · (y, 0) = iy.
, так как (0, y) = (0, 1) · (y, 0) = iy.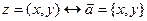 .
.
 , соответствующий комплексному числу z = (x, y) – это радиус-вектор точки (Re z, Im z) (рис. 1).
, соответствующий комплексному числу z = (x, y) – это радиус-вектор точки (Re z, Im z) (рис. 1). , т.е.
, т.е.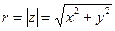
 .
.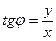 .
.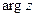 называется то его значение, которое удовлетворяет неравенству
называется то его значение, которое удовлетворяет неравенству 
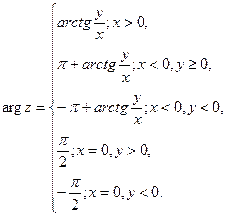
 , обозначается Arg
, обозначается Arg  ,
,