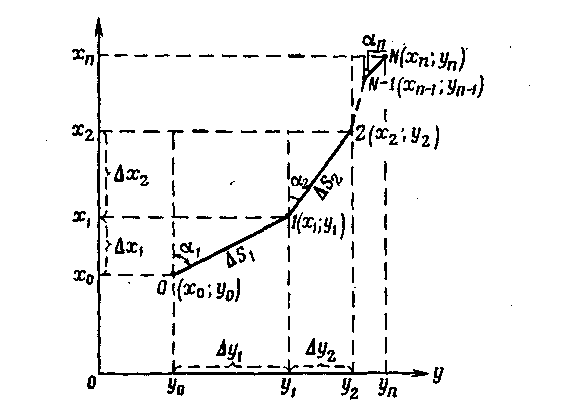
Принцип определения текущих координат движущейся машины.
Работа навигационной аппаратуры сводится к непрерывному измерению проходимого машиной пути и дирекционного угла направления движения и вычислению на основе этих данных координат местоположения движущейся машины. Допустим, движение машины начинается из точки О (рис. 76), координаты которой х0 и у0 известны, например определены по карте. Двигаясь прямолинейно, машина переместилась в точку l. Ее координаты Х1 и у1. Из рисунка видно, что прямоугольные координаты машины в точке / будут: Х1 = X0 + ∆X1 У1 = У0 + ∆У1 Приращения координат ∆X и ∆У зависят от длины пути (AS), пройденного машиной, и направления (а) ее движения. Они вычисляются по формулам: ∆X1= ∆S1cos а1; ∆У1 =∆S1sina1. А потому: Х1 = Х0 + ∆S1cos а1; У1 = Уо + ∆S1 sina1. В следующий момент времени дирекционный угол направления движения машины будет а2, а путь, пройденный ею до точки 2, - ∆S2.
Координаты точки 2 будут: Х2 — Х0 + ∆X1+∆X2 = Хо + ∆S1cos а1 +∆S2cos а2; У2 = Уо + ∆У1 + ∆У2 = Уо + ∆S1 sina1+ =∆S2 sina2
Аналогично для точки N получим: n n Хn=Х0+∆X1+∆X2 +... +∆Xn = Х0 + ∑∆X = Х0 + ∑∆X ∆Scos; 1 1 n n Уn=У0+∆У1+∆У2 +... +∆Уn = У0 + ∑∆У = У0 + ∑∆У ∆Ssina. 1 1
Рис. 76. Зависимость приращений координат ∆X и ∆У от расстояния, пройденного машиной, и дирекционного угла направления движения.
Таким образом, текущие координаты движущейся машины равны алгебраической сумме координат начальной точки и приращений ∆X и ∆У, вычисленных аппаратурой в процессе движения машины от начальной точки до данной.
|