Общая, факторная и остаточная дисперсии
Разделив суммы квадратов отклонений на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии:
где p — число уровней фактора; q — число наблюдений на каждом уровне; pq - 1 — число степеней свободы общей дисперсии; p - 1 — число степеней свободы факторной дисперсии; p(q - 1) — число степеней свободы остаточной дисперсии. Если нулевая гипотеза о равенстве средних справедлива, то все эти дисперсии являются несмещенными оценками генеральной дисперсии. Например, учитывая, что объем выборки n = pq, заключаем, что
- исправленная выборочная дисперсия, которая, как известно, является несмещенной оценкой генеральной дисперсии. Замечание. Число степеней свободы p (q - 1)остаточной дисперсии равно разности между числами степеней свободы обшей и факторной дисперсий. Действительно,
|

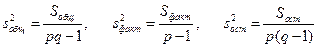

 .
.


