Симплексный метод
Выше были рассмотрены основные теоремы ЛП. Из них следует, что если ЗЛП имеет оптимальное решение, то оно соответствует хотя бы одной точке многогранника решений и совпадает хотя бы с одним из допустимых базисных решений системы ограничений. Там же мы рассмотрели, что путем решения любой ЗЛП является перебор конечного числа допустимых базисных решений системы ограничений и выбор среди них того, на котором функция цели принимает оптимальное значение. Геометрически надо перебрать все угловые точки многогранника решений. Трудно осуществить, т.к. для реальных задач число ДБР хоть и конечно, но м.б. велико. Число перебираемых ДБР можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь, чтобы каждое следующее решение было «лучше» (или, по крайней мере, «не хуже») предыдущего по значению целевой функции.
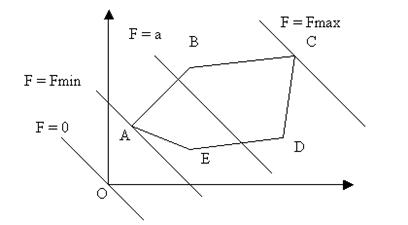
Предположим, точка А – исходное ДБР (допустимое базисное решение). Из чертежа видно, что от А выгодно перейти к В, а потом к С. Идея последовательного улучшения решения легла в основу универсального метода решения ЗЛП – симплексного метода. Впервые был предложен амер. ученым Дж. Данцигом в 1949 г., хотя идеи метода были разработаны Л. В. Канторовичем в 1939 году. Метод используется для компьютерных расчетов. Для реализации метода необходимо освоить три основных элемента: § способ определения первоначального ДБР задачи; § правило перехода к лучшему (не худшему) решению; § критерий проверки оптимальности найденного решения. Для использования симплексного метода ЗЛП д.б. приведена к каноническому виду, т.е. система ограничений – в виде уравнений.
|