Система m линейных уравнений с n переменнымиСистема m линейных уравнений с n переменными имеет вид:
а21*Х1 + а22*Х2 + …+ а2j*Xj + … + а2n*Xn = В2 …………………………. аi1*Х1 + аi2*Х2 +…+ аij*Xj + … + а in*Xn = В i (6) …………………………. аm1*Х1 + аm2*Х2 + … + аmn*Xn = Вm
или в краткой записи
в задачах ЛП представляют интерес системы, в которых максимальное число независимых уравнений системы меньше числа переменных. Будем полагать, что в системе (6) все m уравнений системы независимы, т.е. m < n. Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными (базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (или свободными). Основными могут быть разные группы из n переменных, но общее число групп не превосходит число сочетаний
Пример: Найти все возможные группы основных переменных в системе
2х1 + х2 + 2х3 – х4 = 2
Решение. Общее число групп основных переменных не более чем
Существует теорема. Если для системы из m линейных уравнений с n переменными ((m < n) существует хотя бы одна группа основных переменных, то эта система является неопределенной, причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы. Пусть, например, х1, х2, …, хm – основные переменные (если это не так, то нумерацию можно изменить), то определитель матрицы
Оставим в левых частях уравнений системы (6) члены с переменными х1, х2, …, хm, а члены с переменными xm+1, xm+2, …, xn перенесем в правые части. Получим:
а11*Х1 + а12*Х2 + …+ а1m*Xm = В1 - а1m+1*Xm+1 - … - а1n*Xn а21*Х1 + а22*Х2 + …+ а2m*Xm = В2 – а2m+1*Xm+1 - … - а2n*Xn ……………………………………………………………………. аm1*Х1 + аm2*Х2 + …+ аmm*Xm = Вm - аmm+1*Xm+1 - … - аmn*Xn
Задавая неосновным переменным xm+1, xm+2, …, xn произвольные значения, каждый раз будем получать новую систему с новыми свободными членами. Каждая из полученных систем будет иметь один и тот же определитель, т.е. каждая из систем будет иметь единственное решение. Так как получаемых таким образом систем бесконечное множество, то и система (6) будет иметь бесконечное множество решений. Решение Х = (х1, х2, …, хn) системы (6) называется допустимым, если оно содержит лишь неотрицательные компоненты, т.е. Хj >=0 для любых j = 1, 2, …, n. В противном случае решение называется недопустимым. Среди бесконечного множества решений системы выделяют базисные решения. Базисным решением (БР) системы m линейных уравнений с n переменными называют решение, в котором все n – m неосновных переменных равны нулю. В задачах ЛП особый интерес представляют допустимые базисные решении (ДБР), или, как их еще называют, опорные планы. Число базисных решений является конечным, т.к. оно равно числу групп основных переменных, не превосходящему Пример: В примере (7) существует три группы основных переменных, т.е. число базисных решений = 3. Первое х1 и х2 – основные, х3 и х4 – неосновные (= 0), тогда
2х1 + х2 = 2 откуда х1 =2/3; х2 = 2/3. следовательно первое баз решение системы Х1 = (2/3; 2/3; 0; 0) –допустимое. Если взять за основные переменные Х1 и Х3, то получим второе баз решение системы Х2 = (2/3; 0; 2/3; 0) – также допустимое. Аналогично можно найти третье баз решение при основных переменных х1, х4 Х3 = (2/3; 0; 0; -2/3) – недопустимое. Вывод: Совместная система (6) имеет бесконечно много решений, из них базисных решений – конечное число, не превосходящее
|
а11*Х1 + а12*Х2 + …+ а1j*Xj + …+ а1n*Xn = В1
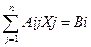(I = 1, 2, …, m)
.
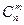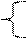х1 – х2 – 2х3 + х4 = 0 (7)
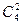= 4*3/2 = 6, т.е. возможны группы основных переменных: х1, х2; х1, х3; х1, х4; х2, х3; х2, х4; х3, х4.
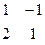= 1 * 1 – 2 * (-1) = 3 ¹ 0. рассуждая аналогично, можно найти, что могут быть основными переменные х1, х3; х1, х4, но не могут быть основными х2, х3; х2, х4; х3, х4, т.к. соответствующие определители равны 0.
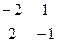= (-2) * (-1) – 2 * 1 = 0.
¹ 0.
